基本情報技術者試験(FE) ～情報の基礎理論「コンピュータの演算」～【第2回】

論理演算（回路記号）

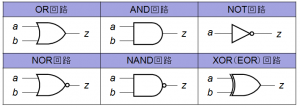
コンピュータには、論理演算を行うための電子回路である論理回路が組み込まれています。各論理演算に対する論理回路は、以下の「MIL記号」で表します。また、各論理回路の動作は、真理値に従って出力結果を出します。

論理演算（加算器）

「加算器」には、2進数1桁の加算を行う回路で、AND回路、OR回路、NOT回路の３つの論理回路から構成されます。そして、下位桁からの桁上がりを考慮しない「半加算器」、下位桁からの桁上がりを考慮する「全加算器」があります。

①半加算器（Half Adder：HA）
「半加算器」は、加算するための回路、「全加算器（full adder)」の構成要素となる回路です。
回路の入力「A」、「B」に「0」または「1」の信号を送ると、加算結果が、出力「C」、「S」に現れます。
「C」は、「carry」の頭文字で、桁上がりを表します。
「S」は、「sum」の頭文字で、加算結果の下位1桁を表します。

2進数の加算結果は、以下の通りとなります。
「C」が「論理積」、「S」が「排他的論理和」となります。

以下図の左側は、半加算器の回路構成です。右側は、半加算器を簡略化したもので、一般的には、この略記表現が使われます。

②全加算器（Full Adder：FA）
複数の桁の加算を行う場合には、下位からの桁上がりも考慮する必要があります。このような下位からの桁上がりを考慮した回路というのが「全加算器」となります。

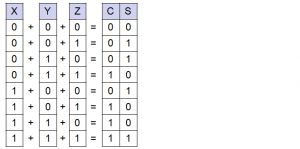
以下は、入力が３つあり、１つは下位桁からの繰上りの例で、「X」、「Y」、「Z」の3つの数の加算となります。この時の加算結果は以下のようになります。
全加算器では、半加算器のような論理積、排他的論理和という関係が成り立ちません。

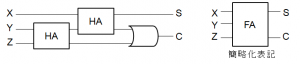
以下図の左側は、全加算器の回路構成です。
半加算器を2つ組み合わせて全加算器を構成しています。また、右側は、全加算器を略したものとなります。