基本情報技術者試験(FE) ~情報の基礎理論「コンピュータのデータ表現」~ 【第3回】
情報の基礎理論
コンピュータのデータ表現 その3
10進数の表現
日常使っている10進数をコンピュータ内部では、様々な形で表現されています。
コンピュータ内部での数値表現には、次のようなものがあります。
①ゾーン10進数
「ゾーン10進数」は、10進数の1桁を「8ビット」で表し、最後の1桁の上位4ビットに「符号情報」を格納します。各バイトの数字ビットには、対応する数値が2進数で格納されます。
・10進数1桁を「8ビット」で表す。
・1桁を表す「8ビット」には、「ゾーンビット(4ビット)」と「数字ビット(4ビット)」を含む。
・最後の桁には、「符号ビット(4ビット)」と「数字ビット(4ビット)」で表す。
・正負を考えない場合は、符号ビットにはゾーンビットと同じものが入る。
⇒ゾーンビット=「1111」または「0011」。データが数値であることを示している。
⇒数字ビット =10進数の値を2進数に変換したものになる。
⇒符号ビット =「1100」か「1101」で表し、「1100」が「正」、「1101」が「負」を表す。
正負を考えない場合は、符号ビットにはゾーンビットと同じものが入る。
10進数「+267」を「ゾーン10進数」で表した場合には、
![]()
10進数「-267」を「ゾーン10進数」で表した場合には、
![]()
②バック10進数
バック10進数は、10進数の1桁を「4ビット」で表し、最後の「4ビット」で符号を表します。1バイトに満たない場合は、0が埋められます。また、「符号ビット」のビットパターンは、ゾーン10進数と同じとなります。
- 10進数の1桁を「4ビット」で表す。
- 最後に「符号ビット」を追加。
- 合計がバイト単位でない場合、先頭に「4ビット」分の「0」を追加。
- 10進数の桁数が 偶数の場合、先頭に「0000」を追加。
10進数の表現(補数)
補数表現は、現在のコンピュータにおいて負数の表現方式として使用しています。
補数表現には、「1の補数」と「2の負数」があります。10進数の数値xに対して、2進数n桁の補数の求め方は、以下のとおりです。

例として、「-10」の補数表現を以下に示します。
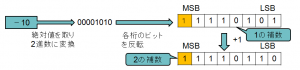
補数表現は、コンピュータで行う減算を加算で実現するために使われています。
つまり、減算(A - B)に対して、Bの値を2の補数を使って(-B )と表し、A+(-B)として計算を行います。
負数の各表現方法をまとめたものを以下に示します。
| 10進数 | 符号付き絶対値表現 | 1の補数 | 2の補数 | |
|---|---|---|---|---|
| 127 | 1111111 | 1111111 | 1111111 | |
| 126 | 1111110 | 1111110 | 1111110 | |
| ・ | ・ | ・ | ・ | |
| +2 | 00000010 | 00000010 | 00000010 | |
| +1 | 00000001 | 00000001 | 00000001 | |
| 0 | +0 | 00000000 | 00000000 | 00000000 |
| -0 | 10000000 | 11111111 | ||
| -1 | 10000001 | 11111110 | 11111111 | |
| -2 | 10000010 | 11111101 | 11111110 | |
| ・ | ・ | ・ | ・ | |
| -127 | 11111111 | 10000000 | 10000010 | |
| -128 | (8ビットでは表現不可) | 10000000 | ||
初級インフラエンジニアにオススメ連載リンク
ネットワーク学習の登竜門・・
ゼロからのCCNA独学講座
Linuxの取り扱いを基礎から学ぶ
Linux資格 「LPIC-Lv1」徹底解説









