目次
- フレームごとの学習処理
- 学習結果
- 学習高速化
- さいごに
■フレームごとの学習処理
フレームごとの処理コード概要を以下に示す。
var qix0 = -1 # 前回の qix
var act0 = 0
var Q = [] # Q値テーブル
func _physics_process(delta):
if !started: return
nSteps += 1
if nSteps >= MAX_STEPS: # 最大ステップ数を超えた場合は現エピソード修了
.....
return
.....
cartPosX = cart.position.x
if cartPosX < MIN_POSX || cartPosX >= MAX_POSX || abs(deg) >= 45: # 範囲外の場合は失敗
.....
else: # カート位置・速度、バー角度が範囲内の場合
var act = 0
var qix = get_qix(cartPosX, cartVel, deg, ddeg)
if qix >= 0 && Q[qix][ACT_LEFT] != Q[qix][ACT_RIGHT]:
# 左右のQ値が異なる場合は、大きい方を行動とする
act = ACT_LEFT if Q[qix][ACT_LEFT] > Q[qix][ACT_RIGHT] else ACT_RIGHT
else: # 左右のQ値が等しい場合は、乱数で行動を決める
act = ACT_LEFT if rng.randf_range(0, 1) < 0.5 else ACT_RIGHT
if act == ACT_LEFT:
cart.apply_central_impulse(Vector2(-20, 0)) # 左方向加速度
else:
cart.apply_central_impulse(Vector2(20, 0)) # 右方向加速度
var reward0 = 1.0 if abs(bar.rotation_degrees) <= 5 else 0.0 # バーがプラマイ5以内なら、報酬 +1.0
# 位置が中央から外れている場合は、報酬をへらす 300 → 0.3
var reward = reward0 - abs(cartPosX - SCREEN_CX) / 1000.0
if qix >= 0 && qix0 >= 0:
var maxQ = Q[qix].max()
var t = min(1.0, reward + GAMMA * maxQ)
Q[qix0][act0] += ALPHA * (t - Q[qix0][act0]) # Q値更新
act0 = act # 行動を保存しておく
qix0 = qix # Q値テーブルインデックスも保存
基本的には、これまで示した例と同じように、下記の式(wikipedia より引用)に従って、Q値を更新する。
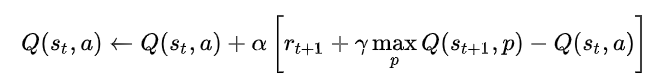
ただし、これまでは1フレーム内で行動した結果をすぐに取得することができたが、 物理シミュレーションでは、行動として台に左右どちらかかの加速度を与えた結果がどうなったのかは、 次のフレームにならないとわからないという点がこれまでと異なる。
したがって、フレーム内で行動を選択したら、それを act0 として保存し、次のフレームで参照する。 Q値テーブルインデックスも同様だ。
■学習結果
以下に、100エピソード学習の最初の1分間の動画を示す。
下記の表・グラフは合計100エピソードの学習を行い、10エピソードごとに振子が何ステップ立っていられたかの平均を計測したものだ。 また、Q値テーブルが更新された割合も計測し、グラフにしている。
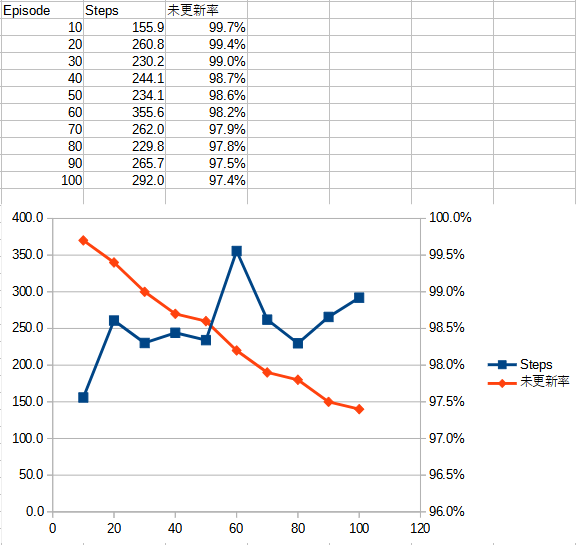
この結果を見ると、Q値テーブルは徐々に更新されており、振子が立っていたステップも概ね上昇してはいることがわかる。 が、実際にアプリを実行してみると、学習の進行が遅い印象を受ける。
実際、100エピソードの学習には約10分間を要した。この間に更新できたQ値テーブルは、わずか 2.5% でしかない。 長く振子が立っていられるようにするには、これよりはるかに多くの時間を要すると推測される。
■学習高速化
学習がなかなか進まないことが不満だったので、学習の高速化を試みてみることにした。
まず、倒立振子は左右対称なので、左側で学習した学習結果を右側にも適用することにした (筆者はこれをミラー学習と呼んでいる)。
コードは単純で、以下のように左右対称位置のQ値テーブルインデックスを求め、 それを更新式で更新しているだけだ。
Q[qix0][act0] += ALPHA * (reward - Q[qix0][act0]) # 通常更新処理
if $Mirror.is_pressed() || $Parallel.is_pressed():
Q[qix0_R][ACT_SUM - act0] = Q[qix0][act0] # ミラー更新処理
.....
qix0_R = get_qix(SCREEN_WIDTH - cartPosX, -cartVel, -deg, -ddeg) # ミラー処理のために、qix を保存しておく
画面にはオプションボタンを設置しているので、それが押されていれば、ミラー更新処理を行っている。
ミラー処理時には行動や、状態(位置、速度、角度、角速度)がマイナスになるのに注意だ。
以下に、ミラー学習を行った場合の100エピソード学習最初の1分間の動画を示す。
下記の値・グラフはミラー学習を行った場合の結果だ。
Q値テーブルの更新率が約倍になり、立っているステップ数もかなり改善されたのがわかる。
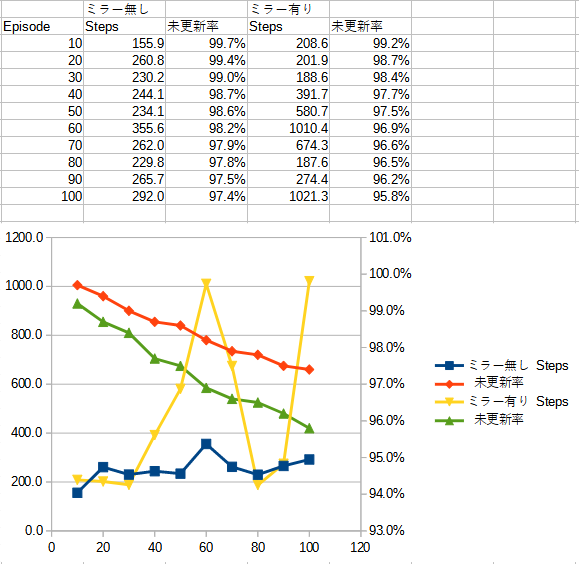
ミラー学習の成果だけでは満足できなかったので、 バー・カートを左右に並行移動した場合についても同様にQ値テーブルを更新するようにしてみた。
ただし、台が中央でバーが立っている方が、台が端の方にあるより優れているのは明らかなので、 台が中央に位置しているほどより高い報酬を与えるようにした。
コードは以下のような感じだ。
func parallel_move_learning(qix, reward0):
if !$Parallel.is_pressed(): return
var qx = qix - QIX_POS_OFFSET
var qx0 = qix0 - QIX_POS_OFFSET
var cx = cartPosX - CART_POSX_STEP
var qx0R = qix0_R + QIX_POS_OFFSET
while qx >= 0 && qx0 >= 0:
var reward = reward0 - abs(cartPosX - SCREEN_CX) / 1000.0 # 300 → 0.3
var t2 = min(1.0, reward + GAMMA * Q[qx].max())
Q[qx0][act0] += ALPHA * (t2 - Q[qx0][act0])
if qx0R < Q.size():
Q[qx0R][ACT_SUM - act0] = Q[qx0][act0]
qx -= QIX_POS_OFFSET
qx0 -= QIX_POS_OFFSET
cx -= CART_POSX_STEP
qx0R += QIX_POS_OFFSET
.....
以下に、ミラー学習+並行移動学習を行った場合の100エピソード学習最初の1分間の動画を示す。
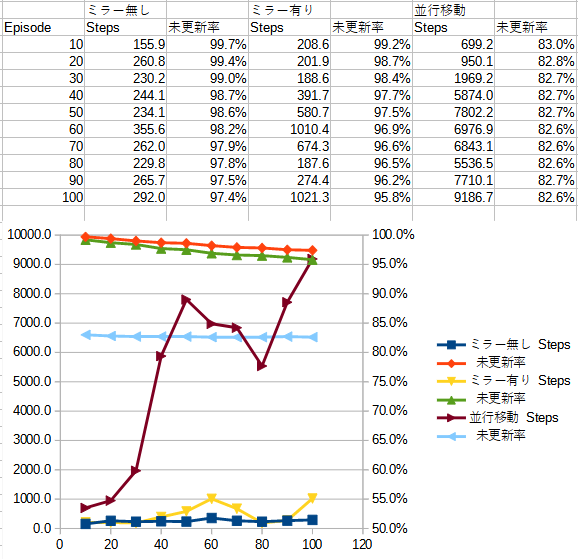
下記の表・グラフはミラー学習+並行移動学習を行った場合の結果だ。
並行移動により、1ステップで数10のQ値を同時に更新できるので、これまでより学習速度がはるかに高速になり、 少ないエピソード数でも長い時間バーを立てていられるようになった。個人的には満足だ。
さいごに
Godot を使って、迷路脱出、三目並べ、倒立振子を題材にしたQ学習のアプリを実装し、実験してみた。
ある程度難しい問題においては学習は期待したようには進まなかったが、 いろいろな工夫をすることで満足できる機会学習を実装できたと考えている。
エージェントが最初は愚かな行動ばかりするのだが、それがだんだん改善されていくのを見るのは、 動物の赤ちゃんの成長を見ているようで、なんとなく楽しいものだった。
機械学習に興味がある読者は、ぜひ何かのモデルで実装し、試してみてほしいと思っている。
「はじめに」にも書いたが、このような試行錯誤を行うシステムの実装には、 生産性がかなり高い Godot はかなり最適なのではないかと考えている。
TechProjin Godot入門 関連連載リンク
Godotで学ぶゲーム制作
さくさく理解するGodot入門 連載目次
標準C++ライブラリの活用でコーディング力UP!
「競技プログラミング風」標準C++ライブラリ 連載目次




