目次
- 倒立振子
- 概要
- 倒立振子状態・行動
- 画面(UI)作成
- 初期化処理
- 学習開始
倒立振子
■概要
Godot で Q学習を実装・解説の最後として、下図のような倒立振子を題材としてみる。
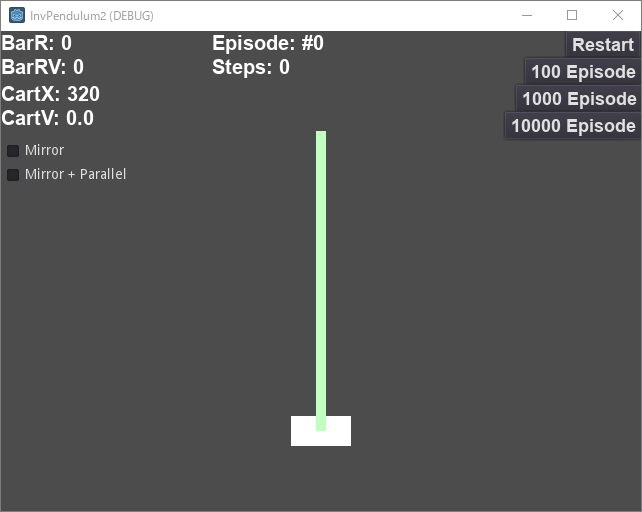
倒立振子とは、下部の台に連結された棒が倒れないように、台を水平に移動制御(正確には加速制御)することだ。
多くの人は子供のときにホウキを手のひらに立てて、それが倒れないように遊んだことがあると思う。 それをQ学習でやってみようというわけだ。
個人的には、迷路脱出や状態数が非常に少ない三目並べにQ学習を用いる必要性を理解できていない。 なぜなら、単純な経路探索やミニマックス評価を行えば解が瞬時に求まるから、 わざわざ時間やメモリを使って学習する意味が薄いと考えているからだ。
しかし、倒立振子は制御理論を勉強していない筆者にとっては、制御アルゴリズムを具体的にどうするのかがさっぱりわからないので、 実装する意味があると考えている。
なお、例によって本稿の全ソースは github(https://github.com/vivisuke/InvPendulum2) にアップしているので、ぜひダウンロードして実際に修正・実行などを行ってほしい。
■倒立振子状態・行動
バーの角度・角速度、カートのX軸方向位置・加速度を、倒立振子の状態として持つ。 ただし、分解能を高くすると状態数が多くなり学習に膨大な時間を要するので、それらを粗い状態に分ける。
具体的には、バー角度は時計回り方向がプラスで、まっすぐ立っている状態を0度とし、10度単位に四捨五入して -40度~+40度の範囲とする。 45度を超えた場合はバーが倒れたと判定する。したがって、角度の状態数は11となる。
バー角速度は5度/秒単位とし、-25~+25の範囲とする。この範囲を超えた場合は、-25 または +25 の状態と同一とする。 したがって、角速度の状態数も11だ。
ついで、カート位置は10px単位とする。画面横幅は 640px にし、端の位置にカートが来た場合はバーが直立していても失敗とみなす。 したがって、カート位置の状態数は63となる。
最後にカート速度は 0.2px/秒単位で、-1.0 ~ +1.0 の範囲とする。この範囲を超えた場合は -1.0 または +1.0 とみなす。 したがって、カート速度の状態数も11だ。
以上の状態はすべて独立なので、全体の状態数は 11 * 11 * 63 * 11 = 83,853 となる。
可能な行動は倒立振子の土台(カート)に左向きか右向きの定数加速度を与える、の2種類としている。 加速度無しというのもあってもいいかもしれないが、その分Q値テーブルの要素数が増え、学習により多くの時間を要するようになるので、 本稿アプリでは、かならずどちらかの方向に定数加速度を与えるものとした。
よって、Q値テーブルの要素数は 83853 * 2 = 167,706 となり、Q値すべてを配列で保持しても問題がないことになる。
このように状態・行動の精度が荒いと学習時間は短くなるのだが、バーをきめ細かく制御することはできなくなり、 ピタリと直立させるのは困難になる。このあたりはトレードオフだ。
■画面(UI)作成
画面に配置する倒立振子に関係する部分は下図のような構成になっている。
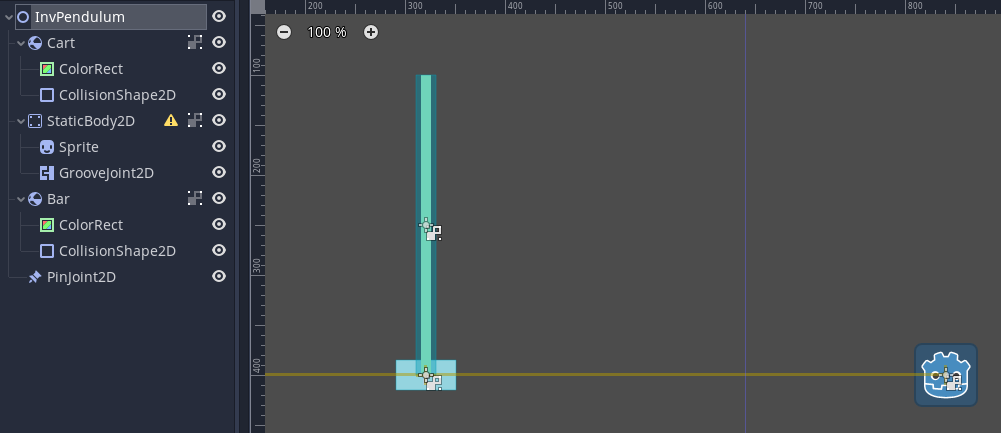
画面右外側に、位置固定の StaticBody を配置し、そこから画面内に向かって GrooveJoint2D を配置。 GrooveJoint2D は直線上にオブジェクトをスライドさせることができるものだ。
下図のように、インスペクターで Joint2D 部分に画面右外の StaticBody と、水平に移動する Cart を連結している。
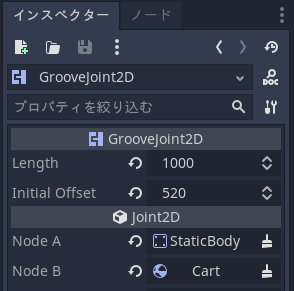
左右に移動するカート、倒立振子部分は RigidBody2D とし、形状として ColorRect を、衝突判定用として CollisionShape2D オブジェクトを配置している。
そして、Pinjoint2D オブジェクトを使って、カートと倒立振子を関節でつないでいる。
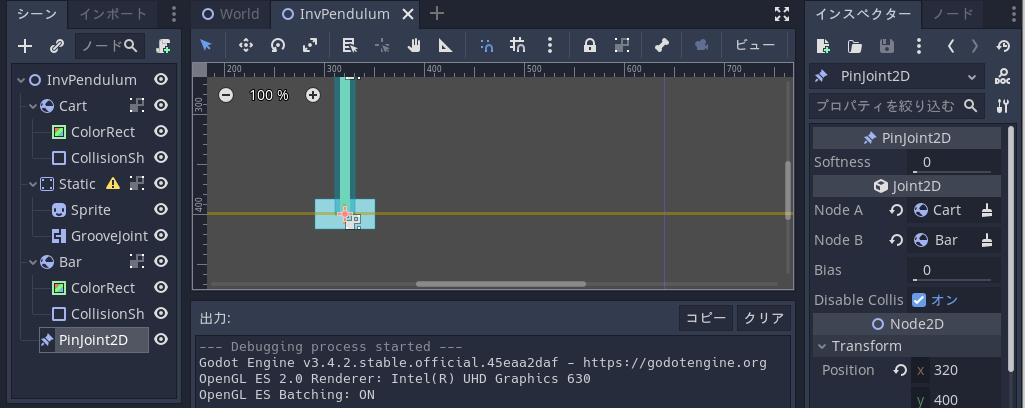
メインシーンは World.tscn で、下図のように情報表示用ラベルと操作用のボタンを配置しているだけ。

初期化処理時に、先の倒立振子シーンをインスタンス化し、画面に追加する(次節参照)。 このような方式にしているのは、1エピソードが修了したときの倒立振子初期化が面倒だったので、 現状のものを削除し、新しいオブジェクトをインスタンスする方が安全確実だと判断したからだ。
■初期化処理
下記に初期化コードを示す。
func _ready():
rng.randomize() # 乱数シードをランダムに
Q.resize(QT_SIZE)
# 楽観的初期値
for i in range(Q.size()): Q[i] = [1.0, 1.0] # X軸方向 [0] for マイナス、[1] for プラス加速度
init_node() # 倒立振子を画面に追加
qix_org = get_qix(SCREEN_CX, 0, 0, 0) # 状態 → Q値テーブルインデックス計算
rng.randomize() で、乱数シードをランダムにし、Q値テーブルを楽観的初期値で初期化している。 Q値配列の要素は2要素の配列になっており、最初の要素はX軸方向にマイナス加速度を与える場合のQ値を、 2番めの要素はX軸方向にマイナス加速度を与える場合のQ値を表す。 本稿アプリでは ε-greedy 法を使わず、Q値を最大値の1.0にしておくことで、すべての可能性を試す楽観的初期値法を用いている。
以下に、倒立振子を画面に追加する init_node() のコードを示す。
var InvPendulum = load("res://InvPendulum.tscn")
func init_node(): # 倒立振子を画面に追加
node = InvPendulum.instance() # 倒立振子シーンをインスタンス化
add_child(node) # 現シーンに追加
cart = node.get_node("Cart") # カートオブジェクト
cartPosX = cart.position.x # カート位置
bar = node.get_node("Bar")
barDeg = 0.0 # 振り子角度
center_pix = cartPosX_to_pix(SCREEN_CX) #
InvPendulum.instance() で倒立振子シーンをインスタンス化し、現シーンに追加している。
各オブジェクトを後で簡単に参照できるように、メンバ変数に参照をコピーしている。
下記に、状態からQ値テーブルインデクスを求める get_qix(cartPosX, cartVel, deg, ddeg) 関数のコードを示す。
func get_qix(cartPosX, cartVel, deg, ddeg):
var pix : int = clamp(round((cartPosX - MIN_POSX) / CART_POSX_STEP), 0, N_POSX-1)
var vix : int = clamp(round(cartVel*5.0) + 5, 0, N_VEL-1)
var aix : int = clamp(round(deg / 10.0) + 4, 0, N_ANGLE-1)
var avix : int = clamp(round(ddeg / 5.0) + 5, 0, N_ANGLE_VEL-1)
return (((pix * N_VEL) + vix) * N_ANGLE + aix) * N_ANGLE_VEL + avix
カート位置・速度、バー角度・角速度の各状態を離散化し、それらを乗じて加えてQ値テーブルインデックスを計算している。
■学習開始
下記に学習開始処理のコードを示す。
func doStart():
node.queue_free()
init_node()
nEpisode += 1
$RoundLabel.text = "Episode: #%d" % nEpisode
score = 0
qix0 = -1
started = true
nSteps = 0
lstQIX = [] # qix 履歴クリア
func _on_100RoundButton_pressed(): # 100エピソード学習開始
nEpisodeRest = 100
doStart() # スタート処理
画面右上の「100 Episode」ボタンが押下されると、press シグナルに接続された _on_100RoundButton_pressed() がコールされる。 そこで、エピソード数が 100 に設定され、doStart() が呼ばれる。
doStart() では古い倒立振子ノードを削除し、init_node() を呼んで新たに倒立振子ノードを作成する。 その他には、スコアやステップ数などを初期化し、started フラグを true に設定している。
started フラグは、次節で説明する _physics_process(delta) で参照され、true であれば物理シミュレーションとQ学習が行われる。
TechProjin Godot入門 関連連載リンク
Godotで学ぶゲーム制作
さくさく理解するGodot入門 連載目次
標準C++ライブラリの活用でコーディング力UP!
「競技プログラミング風」標準C++ライブラリ 連載目次




