目次
- フレームごとの処理
- 学習結果
■フレームごとの処理
Godot では各フレーム(通常60FPS)ごとに _process(delta) がコールされるので、 その中で下記のように mode をチェックし、AI 対 ランダム 対戦モードであれば、modeAiRand() をコールする。
func _process(delta):
if mode == MODE_RAND_RAND:
modeRandRand() # ランダム vs ランダム
elif mode == MODE_AI_RAND:
modeAiRand() # AI vs ランダム
elif mode == MODE_AI_AI:
modeAiAi() # AI vs AI
modeAiRand() の実装を下記に示す。
func modeAiRand(): # AI vs RAND、学習あり
nEpisode += 1
# nEpisode が奇数の場合は AI が先手(O)、偶数であれば AIが後手(X)
$EpiNumLabel.text = "#%d" % nEpisode
init_board()
var AIturn : bool = (nEpisode & 1) != 0
while true: # 1 フレームで終局までプレイ
nEpisode += 1
$EpiNumLabel.text = "#%d" % nEpisode
init_board()
# nEpisode が奇数の場合は AI が先手(O)、偶数であれば AIが後手(X)
var AIturn : bool = (nEpisode & 1) != 0
var gof = false # 終局(ゲームオーバー)フラグ
while !gof: # 1 フレームで終局までプレイ
var qix = bb_to_qix(bits_O, bits_X) # 現在状態のQ値テーブルインデックス取得
make_Q(qix)
var ix = nextAIMove(qix) if rng.randf_range(0, 1.0) <= 0.9 else nextRandMove() # ε: 10%
#var ix = nextAIMove(qix) if rng.randf_range(0, 1.0) <= 0.99 else nextRandMove() # ε: 1%
var t = ix_to_xy(ix)
set_cell(t[0], t[1], next) # 盤面 TileMap 更新
next = (TILE_O + TILE_X) - next # 手番交代
AIturn = !AIturn
reward = 0.0
gof = is_game_over() # 終局チェック&reward 設定
var qix2 = bb_to_qix(bits_O, bits_X)
make_Q(qix2)
var minmaxQ = 0.0
if !gof:
if next == TILE_O:
minmaxQ = Q[qix2].max()
else:
minmaxQ = Q[qix2].min()
Q[qix][ix] += ALPHA * (reward + GAMMA * minmaxQ - Q[qix][ix]) # Q値テーブル更新
update_nextLabel()
update_qvLabels()
nEpisodeRest -= 1
if !nEpisodeRest: # 指定エピソード回数の学習終了 → 結果表示
mode = MODE_NONE
print("\nnAIwon = %d (%.1f%%)" % [nAIwon, nAIwon * 100.0/nEpisode])
print("nRANDwon = %d (%.1f%%)" % [nRANDwon, nRANDwon * 100.0/nEpisode])
print("nDraw = %d (%.1f%%)" % [nDraw, nDraw * 100.0/nEpisode])
三目並べの処理はかなり軽く、最長でも9手で終局となるので、1フレームで終局に至るまでプレイしている。
最初に終局フラグ gof を false にしておき、gof = is_game_over() で終局判定を行い、while !gof で終局になるまでループしている。
bb_to_qix() はビットボードで表された盤面状態を Q値テーブルのインデックスに変換する関数で、その実装は後で示す。 Q値テーブルは盤面状態ごとに配列の要素を持ち、その配列の各要素は盤面の 0~8 の箇所に石を打った場合の Q値を保持する。 nextAIMove(qix) はそのQ値を参照し、最も大きいQ値の行動を選択する。
本アプリでは、局所解に陥るのを防ぐために ε-greedy アルゴリズムを採用している。 乱数を発生させ 10% の確率で、着手をランダムに決めている。90% の確率で nextAIMove() をコールしている。
is_game_over() で終局かどうかをチェックし、終局している場合は報酬 reward を設定する。
そして最後にQ学習の更新式に従い Q値テーブルを更新している。
以下に nextAIMove() の実装を示す。
func nextAIMove(qix):
var empty = ~(bits_O | bits_X) # 1 for EMPTY
var lst = []
var mask = 1
if next == TILE_O: # O の手番、最大Q値の行動を選択
var maxq = -9
for i in range(Q[qix].size()):
if (empty & mask) != 0:
if Q[qix][i] > maxq:
lst = [i]
maxq = Q[qix][i]
elif Q[qix][i] == maxq:
lst.push_back(i)
mask <<= 1
else: # X の手番、最小Q値の行動を選択
.....
if lst.size() == 1: # 最大値の着手位置が一箇所の場合
return lst[0]
else:
return lst[rng.randi_range(0, lst.size() - 1)]
現在の空欄箇所にしていて、Q値テーブルを調べ、最大値を持つ着手位置を返す。 最大値を持つ着手位置が複数ある場合は、その中からランダムに選んでいる。
終局チェックを行う is_game_over() の実装を以下に示す。
func is_game_over(): # 終局チェック
var gof = false
if is_victory_table[bits_O]: # O が3つ並んでいる場合
if (nEpisode & 1) != 0: # AI が先手(O)
nAIwon += 1
else:
nRANDwon += 1
reward = 1.0
gof = true
elif is_victory_table[bits_X]: # X が3つ並んでいる場合
.....
elif is_draw():
nDraw += 1
gof = true
return gof
func is_draw():
return (bits_O | bits_X) == ALL_BITS # 盤面がすべて埋まっているか?
事前に作成しておいた is_victory_table テーブルを使って、石が3つ並んだかどうかをチェックする。 ついでに、統計情報を更新し、reward(報酬)の値も設定している。
bb_to_qix(bO, bX) はビットボードで表された盤面状態を Q値テーブルのインデックスに変換する関数だ。 各セルは、空、○、☓ の3種類の状態があるので、それぞれを 0, 1, 2 の値とし、3倍しながら合計していき、 テーブルのインデックスとしている。
func bb_to_qix(bO, bX): # 盤面状態(ビットボード)→ Q値テーブルインデックス
var qix = 0
var mask = 1 << 8
while mask != 0:
qix *= 3
if (bO & mask) != 0:
qix += 1
elif (bX & mask) != 0:
qix += 2
mask >>= 1
return qix
■学習結果
1000エピソード(ラウンド)ごとに1万エピソードまで学習させた場合の、AI の対ランダムプレイヤー勝率を下表・図に示す。 1万エピソードの学習で、約80%まで勝率が上がった。
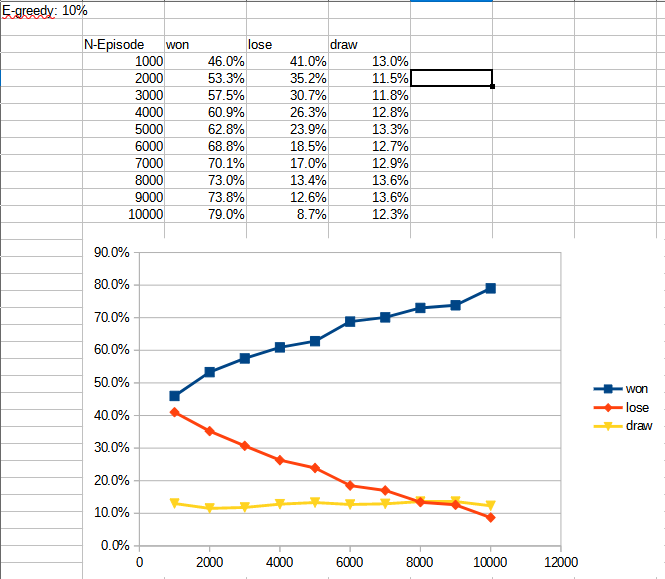
1万エピソードごとに6万エピソードまで学習させた場合の、AI の勝率を下表・図に示す

2~3万エピソードで勝率の増加が90%弱で頭打ちになっていることがわかる。
ここではランダム選択確率の ε を 10% にした場合にみを示しているが、 εが小さいほど学習結果が正確になるが、その反面、学習に必要なエピソード数が増えることになる。 εが大きければその逆だ。
本アプリでは1エピソード/1フレームなので1秒間に60エピソードの学習を行うが、 それでも数万エピソードの学習を行うにはそれなりの時間を要した。
このように学習時間を要するという問題はあるものの、三目並べ程度の状態・着手可能数程度のボードゲームであれば、 Q学習で十分な強さのゲームAIを実装することが可能であることを確認できた。
TechProjin Godot入門 関連連載リンク
Godotで学ぶゲーム制作
さくさく理解するGodot入門 連載目次
標準C++ライブラリの活用でコーディング力UP!
「競技プログラミング風」標準C++ライブラリ 連載目次




