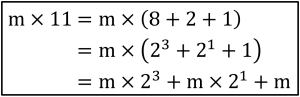今回は【基礎理論編】進数のシフト演算について紹介します。
シフト演算とは左右にビットをズラして掛け算や割り算をすることです。
コンピュータ内部ではこのシフト演算を使って掛け算や割り算を行っています。
実は前回の記事内で、正規化をする際にしれっと使っていました。
例えば10進数の1.89という数に×10をすると、各桁を1つずつ左にずらして18.9となりますね?
×100(×10²)なら2つズラして189、×1/10(×10⁻¹)なら逆方向に1桁ズラして0.189と、10進数において×10^n(nは整数)は簡単に求めることができます。
2進数も同様で、×2^n(←ここは10進数で表記しています。)の計算は各ビット(桁)をnビットずつズラすことで求めることができます。
nが正の数なら左にズレて、負の数なら右にズレます。
『小数点が動いている』と考える場合、動く方向は逆になりますね。
これがシフト演算です。
ビットをズラすことを『シフト』と言います。
シフト演算には『論理シフト』と『算術シフト』があります。
論理シフト
まずは論理シフトについて説明していきます。
論理シフトは符号を考慮しないシフト演算です。
そのため、符号なしのデータの演算に使用されます。
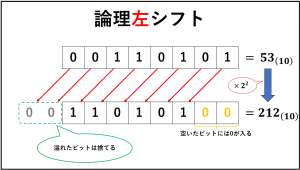
×2²や×2³など、指数部分が正の数の時は数字が左にズレることから『論理左シフト』といいます。
論理左シフトでは、シフトしたことにより空いたビットには0が入ります。
また、コンピュータ内部では指定されたビット数で数値を表現しているため、シフトするとその分溢れることになります。
溢れたビットは捨てられるのですが、論理左シフトの場合、1が溢れると表現不可の数値になり『オーバーフロー』となってしまいます。
論理左シフトがあればもちろん『論理右シフト』もあります。
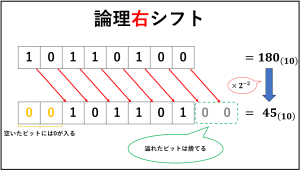
×2⁻²や×2⁻³など、指数部分が負の数の時は数字が右にズレることから論理右シフトといいます。
論理右シフトでも、シフトしたことにより空いたビットには0が入ります。
また論理右シフトの場合、1が溢れるとそれが『余り』となります。
×2⁻²は÷4と同義ですので、計算としては整数の割り算をしていることになります。
そのため、『余り』として処理することができるのです。
算術シフト
続いて算術シフトについて説明していきます。
算術シフトは符号を考慮するシフト演算です。
そのため、符号つきのデータの演算に使用されます。
符号付きのデータでは最上位のビットで符号を表現している(よくわからない方は補数の記事を読んでおきましょう)ため、そのビットはシフトを行いません。
また、論理シフトと同様に『算術左シフト』と『算術右シフト』が存在しますが、算術シフトは論理シフトと違い、左シフトと右シフトとでは空いたビットへの対応が異なります。
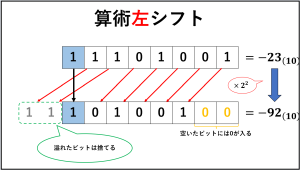
算術左シフトは論理シフトと同様、溢れたビットは捨てて、空いたビットには0が入ります。
論理左シフトとの違いは符号ビット(最上位のビット)を固定することだけです。
正の数の場合は論理左シフトと同様、1が溢れると『オーバーフロー』となります。
負の数の場合は逆に0が溢れると表現不可の数値になり、『オーバーフロー』となります。
補数をちゃんと理解していれば想像がつくはずです。
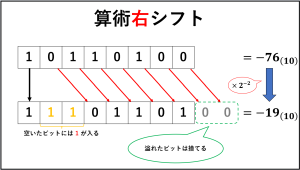
続いて算術右シフトですが、算術右シフトは今まで紹介したシフト演算と異なり、空いたビットには『1』が入ります。
空いたビットが『1』になるのも補数を理解していれば当然のことかと思います。
逆に納得いかないようであれば補数の理解が足りていません。
もう一度補数を学習し直してください。→補数やり直しの方はこちら
溢れたビットの扱いは論理右シフトと同様です。
1が溢れるとそれが割り算の『余り』となります。
シフト演算と加算の組み合わせ
ここまでシフト演算について学び、×2^nの計算は容易にできることがわかりましたね?
しかし、他のかけ算のやり方については学んでいません。
「シフト演算だけできてもあんまり意味なくない?」と思いながら記事を読んでいた方も多いと思います。
当然×2^n以外の計算も必要なのですが、それもシフト演算を利用することで求めることができるのです。
シフト演算と加算(足し算)を組み合わせることで、わりと簡単に計算ができます!
例えば『×11』であれば下図のように変形することにより、シフト演算と加算の組み合わせで計算ができます。
mは任意の2進数です。
こうすれば『mを3桁左シフトしたもの+mを1桁左シフトしたもの+m』という加算でm×11の値を求めることができますね。
まとめ
- シフト演算とは左右にビットをズラして掛け算や割り算をすること
- 論理シフトは符号を考慮しないシフト演算
- 算術シフトは符号を考慮しないシフト演算
- シフト演算と足し算を使えば、基数のべき乗以外の掛け算も計算できる
演習問題
1.正の2進数(整数)を左に3ビットシフトした数は、元の数の何倍になりますか?
A.30
B.6
C.8
D.0.125
2.次の選択肢のうち、10進数の計算13×17の結果を2進数8ビット(符号部無し)で表したものはどれですか?
A.11011101
B.『オーバーフロー』が起きてしまうため表せない
C.11010011
D.01110011
演習問題の解答は次回の記事で
前回の演習問題の解答
1.次の選択肢のうち、10進数-11.375を8ビット固定小数点形式による2進数で表したものはどれですか?小数点の位置は右端から数えて4つ目(小数部分が3ビット分)とし、負の数は2の補数表現を用いてください。
A.10100100
B.11011011
C.11011100
D.10100101
解答:D
解説:小数点の位置を考慮しつつ、11.375を2進数8ビットに変換する⇒01011.011
負の数なので、01011011の2の補数をとる(ビットを反転させて1を加える)⇒10100100(ビット反転)⇒10100101(1を加える)
よって解答はD
2.次の選択肢のうち、10進数-58.5を符号部が1ビット、指数部が7ビット、仮数部が8ビットの浮動小数点形式で表現したものはどれですか?ただし、指数部は実際の指数に64を足したものとする。
A.1110001000110101
B.1110101001000101
C.1110101010001010
D.1100010111010100
解答:D
解説:負の数なので符号部(最上位ビット)は1
58.5を10進数に変換⇒111010.1
正規化⇒1.110101×2⁵
1.110101の小数部分が仮数部(下位8ビット)となる。小数部分が6ビットしかないので、下位2ビットは0で埋める
⇒1〇〇〇〇〇〇〇11010100
2の指数になっている5に64を足し、2進数に変換⇒5+64=69⇒1000101
指数部に当てはめる⇒1100010111010100
よって解答はD