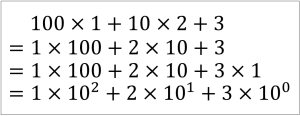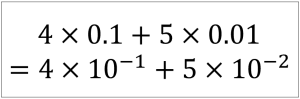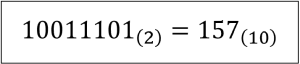今回は【基礎理論編】基数変換について紹介します。
前回の記事で進数について説明をしました。
基数変換は進数の理解が必須です。
今回の記事は読者が進数の概念を理解している体で書いています。
進数についての理解が怪しい方は、前回の記事を読んでから基数変換の学習に進みましょう。
基数とは
いきなり基数変換といわれても「そもそも基数って何?」と思う方もいらっしゃいますよね?
というわけでまずは『基数』について説明していきます。
『基数』とは、各桁の重み付けの基本となる数のことです。
この説明だけではわかりづらいと思うので、『10進数』を例に挙げて説明します。
『10進数』の 123 について考えてみましょう。
123 は百の位が 1 、十の位が 2 、一の位が 3 の3桁の整数です。
中学数学(義務教育)を思い出していただきたいのですが、百の位がa、十の位がb、一の位がcである3桁の整数を式で表すと
100a+10b+c
でしたね。
つまり 123 は百の位が 1 、十の位が 2 、一の位が 3 の3桁の整数なので
100×1 + 10×2 + 3
と表すことができます。
わかりやすくするために式を変形していきます。
このように変形すると、それぞれの桁の数字に10の整数乗がかけられてると考えることができます。
この 10 が基数です。
『10進数』の基数は 10 なのです。
一の位、十の位、百の位、…
という表現をしますが、これは言い換えると
10の0乗の位、10の1乗の位、10の2乗の位、…
です。
123 という整数を例に挙げましたが、これは整数に限った話ではありません。
例えば『10進数』の 0.45 は
と表すことができます。
小数第一位は10の-1乗の位、小数第二位は10の-2乗の位ということになります。
皆様お察しだと思いますが、『10進数』の基数が 10 ということは、『2進数』の基数は 2、『8進数』の基数は 8、『16進数』の基数は 16 です。
長々と『基数』について説明してきましたが、結局「n進数の基数はn」なのです。
「それ最初に言ってよ・・・」と思った方もいるかもしれませんが、そうするとそこだけ切り取ってインプットしようとする浅はかな人間が今後ついてこれなくなってしまいます。
結論だけ覚えていても「基数とはなんなのか」がわからないと無意味なので、超シンプルな結論を後回しにしてネチネチ説明させていただきました。
基数変換
では基数変換の話に入ります。
基数変換とは、ある進数で表現されている数値を、別の進数に変換することです。
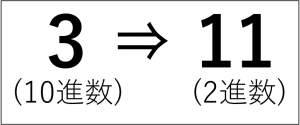
例えば『10進数』の 3 という数は、『2進数』で表すと 11 です。
これが基数変換です。
今回は『2進数』から『10進数』、『2進数』から『8進数』、『2進数』から『16進数』、『10進数』から『2進数』への基数変換を扱いっていきます。
2進数→10進数
2進数を10進数に変換するためには、まず「2進数では各桁が何の位になるのか」を把握している必要があります。
10進数では各桁のことを一の位、十の位、百の位、…と言いました。
そしてこれは10の0乗の位、10の1乗の位、10の2乗の位、…と言い換えることができるという話をしました。
2進数ではこれが2の0乗の位、2の1乗の位、2の2乗の位、…となります。
すなわち一の位、二の位、四の位、…です。
それさえわかればあとは足し算をするだけで2進数から10進数に変換することができます。
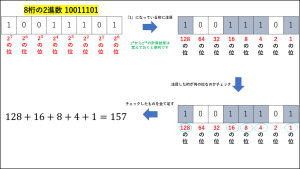
8桁の2進数 10011101 という具体例を使って説明します。
↑あまり見かけませんが、n進数で表されていることがわかるように、
 という表記をすることがあります。
という表記をすることがあります。
2進数から10進数の変換はたったこれだけです。
暗算でも余裕でできるレベルですね。
2進数→8進数
2進数から10進数への変換ができれば、2進数から8進数への変換は少し工夫するだけで簡単にできます。
前回の記事で書きましたが、8進数や16進数は2進数と相性がいいため、計算が非常に楽です。
具体的にどのように楽になるかというと、8進数の1桁が2進数の3桁とリンクしてくれるのです。
8進数は0~7の数字を使うため、1桁で8通りの数を表すことができます。
3桁の2進数で表すことのできる数も 000,001,010,011,100,101,110,111 の8通りです。(全部書き出さなくても2³で求められます)
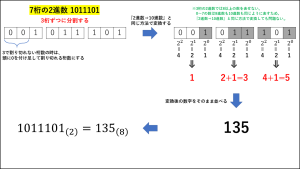
つまり2進数を3桁ずつに区切り、それぞれを8進数に変換すれば良いのです。
7桁の2進数 1011101 という具体例を使って説明します。
簡単ですね。
2進数→16進数
2進数から16進数への変換も2進数から8進数への変換とほぼ同じです。
16進数の1桁は2進数の4桁とリンクしているため、4桁ずつに区切って変換していきます。
ただし、4桁の2進数は0~15の数を表すことができ、10以上の数は10進数と16進数で表し方が異なるため、そこだけ再度変換する必要があります。
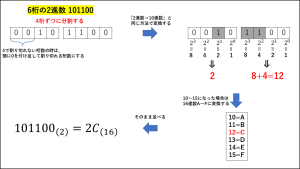
10進数の10,11,12,13,14,15は16進数ではA,B,C,D,E,Fと表されます。
これを踏まえて変換していきましょう。
今回は6桁の2進数 101100 という具体例を使って説明します。
10進数だと『2C』という表現は『2×C』を表すので違和感がありますね。
慣れてください。
10進数→2進数
最後に10進数から2進数の変換です。
前の3つに比べると少し計算が面倒になりますが、難しいものではないのでご安心ください。
引き算ができれば誰でもできます。
超大雑把に言えば、『2のn乗で引き続ける』だけです。
3桁の10進数 174 という具体例を使って説明します。
こんな感じです。
小数が含まれている場合も同様に、0になるまで2の-1乗(0.5)から順番に引き算をしていけばOKです。
基数変換については以上となります。
慣れるまでとにかく計算量をこなしてください。
計算の方法は人それぞれなので、今回紹介した方法に固執する必要はありません。
自分で考えて最善の計算方法を見つけてください。
問題によって工夫すれば計算が楽になることもありますが、楽な計算方法は正しく理解した上でやらないとミスの原因になりますのであえて紹介しません。
自ら編み出してください。
まとめ
- n進数の基数はn
- 2進数から10進数への変換は1になっている桁を足すだけ
- 8進数から10進数への変換は3桁ずつ、16進数から10進数への変換は4桁ずつに区切って計算する
- 10進数から2進数への変換は0になるまでひたすら2の累乗を引きまくる
演習問題
1.『2進数』の 10111111 を『10進数』で表すとどうなりますか?
A.191
B.192
C.254
D.255
2.『2進数』の 10111111 を『16進数』で表すとどうなりますか?
A.4F
B.AE
C.B9
D.BF
3.『10進数』の 247 を『2進数』で表すとどうなりますか?
A.1110111
B.11111000
C.11110111
D.111101111
演習問題の解答は次回の記事で
前回の演習問題の解答
1.『5進数』の 10 を『10進数』で表すとどうなりますか?
A.5
B.6
C.10
解答:A
解説:10という数は、1桁で表すことのできる最大の数に1を足したものです。『5進数』は5種類の数字(0,1,2,3,4)を使うことができるため、『5進数』の10は4に1を加えた数ということになります。よって、『5進数』の10を『10進数』で表すと5です。
2. 2桁の『16進数』で表すことのできる数(1桁だけで表すことのできる数も含む)は何通りありますか?
A.32
B.255
C.256
解答:C
解説:1桁で16通りの数を表すことができるので、2桁あれば16×16で256通りの数を表すことができます。納得がいかない方は『10進数』を考えてみてください。1桁で10通りの数を表すことができる『10進数』は、2桁で0~99の100通りの数を表すことができますよね?10×10=100です。