【基本情報技術者試験】補数

今回は【基礎理論編】補数について紹介します。

前回の記事と前々回の記事は、ほとんどの方にとって高校時代に学習済みの内容でした。
しかし残念ながらここからは多くの方が初見の内容になると思います。
スムーズに頭に入ってこない可能性もありますので、ちょいと気合をいれましょう。

補数とは

では補数について説明していきましょう。
補数とは『ある数』が決められた数になるように『補う数』のことで、コンピュータの内部で負の数を表現する方法の1つです。
『N進数』にはNの補数とN-1の補数があります。
『ある数』にNの補数を補うと、『ある数』より1つ多い桁数の最小値になります。
『ある数』にN-1の補数を補うと、『ある数』と同じ桁数の最大値になります。

この説明で理解できた方もいると思いますが、わかりづらいですね。
こういう時は具体例で理解していきましょう。
最も扱いに慣れているN=10（10進数）を例に、改めて説明していきます。

10進数の補数

3桁の10進数 374 を例に、補数について考えていきます。
N=10ということになりますので、10進数には10の補数（Nの補数）と9の補数（N-1の補数）があります。

まずは10の補数（Nの補数）を求めてみましょう。
374（ある数）に10の補数（Nの補数）を補うと、『ある数』より1つ多い桁数の最小値になるはずです。
この場合の「補う」は、「足す」に言い換えた方が理解し易いかと思います。
また「1つ多い桁数の最小値」もわかりにくいので言い換えましょう。
結局のところ『ある数』が2桁なら 100、3桁なら 1000、4桁なら 10000 ということです。
374 は3桁なので、今回の例の場合は「374に10の補数を足すと1000になる」と言い換えることができます。

つまり、374の10の補数を求めるには「374に何を足したら1000になるか？」を考えるだけでよいのです。
1000-374=626 より、374の10の補数は 626 ということになります。
字面だけで考えると頭に入ってきづらいですが、具体的な数値で考えると非常にシンプルなものです。

続いて9の補数（N-1の補数）を求めましょう。
374（ある数）に9の補数（N-1の補数）を補うと、374（ある数）と同じ桁数の最大値になるはずです。
ごちゃごちゃしているのでさっさと言い換えちゃいましょう。
「同じ桁数の最大値」とは2桁なら99、3桁なら999、4桁なら9999ということです。

つまり、374の9の補数を求めるには「374に何を足したら999になるか？」を考えればOK。
999-374=625 より、374の9の補数は 625 ということになります。

2進数の補数

まだこの時点では補数の存在意義はよくわかりませんが、補数がどのような数なのかは10進数の例でわかったかと思います。
今度は2進数の補数を求めてみましょう。

今回は4ビットの2進数 0110を具体例に説明していきます。
いきなり『ビット』という単位が出てきましたが、細かい説明は【コンピュータシステム編】でする予定ですので、とりあえずは「コンピュータ内部での2進数の桁数」くらいに思っておいてください。
また、最上位の桁が 0 になっていますが、4ビットと言われたら最上位の桁が 0 であろうと、4桁全部使うものだと思ってください。

N=2ということになりますので、2進数には2の補数と1の補数があります。
説明の都合上、1の補数から考えていきます。
2進数は0と1しか使えないので、4ビット（4桁）の2進数の最大値は 1111 です。
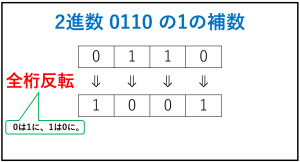
つまり0110に何を足したら1111になるかを考えればよいわけですが、2進数の場合は『ある数』のビットを反転させるだけでOKです。
ここでいう反転は、0を1に、1を0にすることを指します。

よって2進数 0110 の1の補数は 1001 となります。
実際に足してみると 0110 + 1001 = 1111 となり、正しいことがわかります。

では続いて2の補数について考えてみましょう。
皆様既にお気づきだと思いますが、Nの補数は必ずN-1の補数に1を加えたものになります。
10進数の時に考えたのは「何を足せば1000になるか」と「何を足せば999になるか」でしたね。
桁数が変わっても「100と99」や「10000と9999」となるだけですので当然ですね。

もちろんこれは2進数の時も同様です。
そして2進数の場合のN-1の補数（1の補数）は反転だけで簡単に求められるので、N-1の補数を先に扱いました。
その値に1を加えればNの補数になるのです。
というわけで先ほど求めた2進数 0110 の1の補数である 1001 に1を足しちゃいましょう。

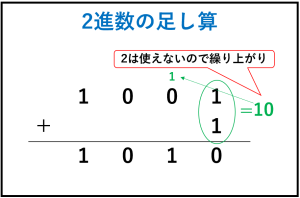
2進数の足し算は慣れていない方もいると思うので、慣れるまでは繰り上がりに注意しながら計算しましょう。
こうして2進数 0110 の2の補数 1010 を求めることができました。
2進数の2の補数を求めたければ、ビットを反転させて1を加えるだけでよいのです。

コンピュータ内部での補数の役割

補数の求め方はわかったかと思いますが、「なぜ補数について学んでいるのか？」はよくわかっていない方が多いと思います。
最後に補数がどのようにコンピュータで使われているのかを説明します。

コンピュータ内部では、2進数の引き算を足し算で処理するために補数が使われています。
例えば4ビットの2進数の計算

1110-0110

を行うとします。
この計算自体はすぐに

1110-0110=1000

と求めることができる思いますが、コンピュータ内部ではこれを足し算で処理しようとします。
『0110を引く』のではなく『0110の2の補数を足す』という処理をします。
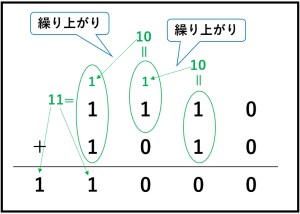
というわけで先ほど求めた1010を1110に足してみましょう。

繰り上げが多く面倒な計算の結果 11000 でした。
でも落ち着いてください。
端末を投げつけるのはまだ早いです。

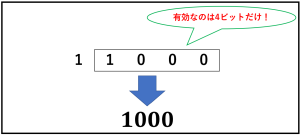
今回は『4ビット』の2進数の話をしています。
計算結果は5桁になってしまいましたので、最上位の桁は無視されます。

これで計算結果が合いましたね。
コンピュータの内部では2の補数を使ってこのような計算を行います。
2進数の2の補数はスムーズに導出できるようにしましょう。

まとめ

2の補数は全てのビットを反転させたものに1を加えれば求められる
コンピュータ内部では2の補数を使って、引き算を足し算で処理している
引く数の2の補数を足し、最上位の桁を無視することで、引き算と同じ計算結果が得られる

演習問題

1.次の選択肢のうち、2進数 10110000 の2の補数はどれですか？

A.01001111
B.01010000
C.10110001
D.01001110

2.次の選択肢のうち、2進数の2の補数で表された負の数 11000101 の絶対値はどれですか？

A.11000100
B.00111011
C.00111010
D.11000101

演習問題の解答は次回の記事で

前回の演習問題の解答

1.『2進数』の 10111111 を『10進数』で表すとどうなりますか？

A.191
B.192
C.254
D.255

解答：A
解説：シンプルに計算するなら128+32+16+8+4+2+1で求められます。
それでも全く問題ありませんが、工夫すると少し計算が楽になります。
2の8乗が256であることから、8桁の2進数で表すことのできる数は0～255であることがわかります。
つまり、8桁の2進数の最大値（11111111）を10進数で表すと255です。
今回は2の6乗の位、すなわち64の位だけが0で、他の位は1なので、255から64を引くだけで191を求めることもできます。

2.『2進数』の 10111111 を『16進数』で表すとどうなりますか？

A.4F
B.AE
C.B9
D.BF

解答：D
解説：2進数から16進数への変換は、4桁ずつに分けて計算します。
まず前半の『1011』は8+2+1=11となり、さらに11を16進数に変換してBとなります。
後半の『1111』は16進数1桁の最大値と同じ数（10進数の15）を表すはずなので、Fとなります。
よってDが正解です。

3.『10進数』の 247 を『2進数』で表すとどうなりますか？

A.1110111
B.11111000
C.11110111
D.111101111

解答：C
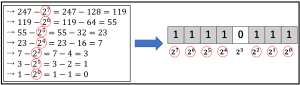
解説：2の7乗が128、2の8乗が256であることから、247を超えない最大の2の累乗は2の7乗であることがわかります。
247から128を引き、あとはひたすら2の累乗で引いていき、位を間違えないように1と0を並べましょう。