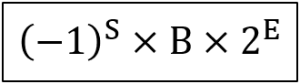今回は【基礎理論編】固定小数点と浮動小数点について紹介します。
前回の記事で、コンピュータの内部では補数によって負の数を表現するということを紹介しました。
今回は小数なども含めた数値の表現方法を紹介します。
コンピュータ内部での数値の表現方法として、固定小数点と浮動小数点というものがあります。
固定小数点
まずは固定小数点について説明していきます。
固定小数点はその名の通り、小数点の位置を固定して数値を表現する方法です。
そのため、事前に小数点の位置が決められているときに使用されます。
コンピュータ内部では、整数を扱うときに使用されています。
固定小数点で整数を扱う場合、小数を一番右端に置くことになります。
また、負の数を扱う場合は左端のビットを符号ビットとし、2の補数表現を使います。→補数についての記事はこちら
例えば2進数8ビットの固定小数点で整数のみを扱う場合は下図のようになります。
2進数8ビットの固定小数点で一番右端に小数点を置いた場合、-128~127の整数を表現することができます。
浮動小数点
続いて浮動小数点について説明していきます。
浮動小数点は指数を使って数値を表現する方法です。
コンピュータ内部で小数を扱う場合に使用されています。
浮動小数点にはいくつかの形式があり、『IEEE754』という形式が最もポピュラーです。
そして『IEEE754』の中にも基数やビット数に応じていくつか形式があります。
今回の記事では、基数を2として32ビットで表現する『単精度』と呼ばれる『IEEE754』の形式を例に説明していきます。
『IEEE754』の『単精度』では、数値を以下のような形で表現すると決められています。
このルールの基で32ビットをS,B,Eに割り振っていきます。
そうすると色々な数が表現できるのですが、ちょっとわかりづらいので一旦10進数で考えてみましょう。
例えば10進数 -0.000125 を10進数のまま上図の形で表すと
となります。
まず(-1)^Sのところで数値の正負を表します。
Sを0にすれば正の数、1にすれば負の数を表すことができますね。
そしてB×10^Eで数値の絶対値を表します。
Bの整数部が0以外の1桁になるように桁を調整しています。
-0.000125は『正負を表す部分+整数1桁+小数6桁』なので、数値を表現するのに合計8つの情報が必要でした。
しかし、変形後は『Sが1桁(0か1)+Bが3桁(整数1桁と小数2桁)+Eが2桁(符号と指数の絶対値)』となり、6つの情報で同じ数値を表すことができています。
数値を表現する形を事前に決めているので、常に一定な部分(S,B,E以外の部分)は情報としてカウントされません。
このように数値を表現する形が決まっていれば、極端に小さな数字や大きな数字は指数を使った方が少ない情報で表現することができます。
違う観点で見ると、同じ情報量が使えるのであれば、指数を使った方がより多くの数字を表現することができるということになりますね。
これはコンピュータにとって大きなメリットです。
では実際にコンピュータ内部で使われている2進数に話を戻しましょう。
Sの部分を『符号部』と言い、32ビットのうち1ビットをここで使用します。
『単精度』以外の形式でも『符号部』は1ビットです。
ここが0なら正の数または0、1なら負の数です。
これは固定小数点や、先ほど例に挙げた10進数と変わりませんね。
Bの部分は『仮数部』と言い、『単精度』では32ビットのうち23ビットをここで使用します。
数値の絶対値を2進数で表したものを『1.〇〇〇・・・』となるように桁を移動したものが入ります。
字面の説明だと少しわかりづらいと思うので、後ほど図で説明します。
Eの部分は『指数部』と言い、『単精度』では32ビットのうち8ビットをここで使用します。
仮数部で桁を移動した分をここで調整しています。
10進数では10のべき乗でしたが、2進数なので2のべき乗で桁の調整ができます。
上記のように『1.〇〇〇・・・となるように桁を移動→べき乗で調整』など、利用しやすくするために一定のルールに基づいてデータを変形することを正規化と言います。
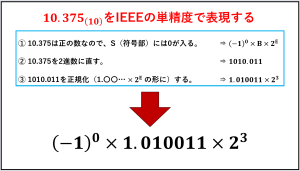
では実際に10進数の10.375を『IEEE754』の『単精度』で表現してみます。
大まかな流れとしては
①符号部を埋める
②絶対値を2進数に変換する →基数変換についてはこちら
③正規化
となります。
S=0, B=1.010011, E=3であることがわかりました。
(2進数に10進数がかけられているのでちょっと気持ち悪いですが、この方が理解しやすいかと思うので気にしなくて大丈夫です)
しかし、これをそのまま
に当てはめることはできませんよね?
Eは思いっきり10進数です。
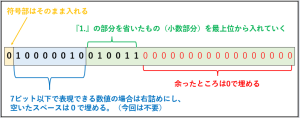
Sはそのまま当てはめるのですが、BとEはもう少し手を加える必要があります。
まずBですが、Bは『小数部分のみ』を当てはめます。
整数部分が必ず1になるように正規化しているので、『1.』の部分を省略しても全く問題がないのです。
これで1桁節約できていますね。
Eは10進数なので当然2進数に変換しなければならないのですが、その前に『127』を足します。
その後2進数に直して当てはめます。
今回であれば3+127=130、そして130を2進数に直して10000010、これを当てはめます。
なぜ『127』を足すのかというと、指数部がマイナスにならないようにするためです。
10進数の例のように、小さい数値(1未満)を表現するときはEがマイナスになります。
『IEEE754』の『単精度』では指数部が8ビットであり、表現できる値は2⁸=256通りです。
負の数も扱うとなると、この『256通り』で『-127~128』を表現するようにしたいですよね?
指数部分の最小である-127に127を足せば0(2進数8ビットで00000000)なので、この方が都合が良いのです。
補数を使えばいいような気もしますが、そこは決まり事なので諦めてください。(2の補数で負の数を表す場合、8ビットで表せるのは-128~127)
127のせいで話がちょっと脱線しましたが、これで無事に全て当てはめることが出来ます。
これで完成です!
『IEEE754』の『単精度』では、これが10進数の10.375を表すことになります。
コンピュータ内部ではこのような形で小数を含んだ数値を表現しています。
確実に変換できるようにしておきましょう!
今回は『IEEE754』の『単精度』という形式を例に説明しましたが、基本情報技術者試験ではオリジナルの形式が出題されることもあります。
問題の指示に沿って考えなくてはならないため、浮動小数点を根本的に理解していくなくてはなりません。
パターン暗記に頼りすぎないように注意してください。
まとめ
- 固定小数点は小数点の位置を固定して数値を表現する方法
- 浮動小数点は指数を使って数値を表現する方法
- 浮動小数点の仮数部は『1.』を省略する
- 浮動小数点の指数部は負の数にならないような数を足してから2進数に直す
演習問題
1.次の選択肢のうち、10進数-11.375を8ビット固定小数点形式による2進数で表したものはどれですか?小数点の位置は右端から数えて4つ目(小数部分が3ビット分)とし、負の数は2の補数表現を用いてください。
A.10100100
B.11011011
C.11011100
D.10100101
2.次の選択肢のうち、10進数-58.5を符号部が1ビット、指数部が7ビット、仮数部が8ビットの浮動小数点形式で表現したものはどれですか?ただし、指数部は実際の指数に64を足したものとする。
A.1110001000110101
B.1110101001000101
C.1110101010001010
D.1100010111010100
演習問題の解答は次回の記事で
前回の演習問題の解答
1.次の選択肢のうち、2進数 10110000 の2の補数はどれですか?
A.01001111
B.01010000
C.10110001
D.01001110
解答:B
解説:前回の記事で紹介したように、全てのビットを反転させたものに1を加えれば2の補数を求めることができます。
したがって、
10110000
↓反転
01001111
↓1を加える
01010000
となり、解答はBとなります。
2.次の選択肢のうち、2進数の2の補数で表された負の数 11000101 の絶対値はどれですか?
A.11000100
B.00111011
C.00111010
D.11000101
解答:B
解説:2の補数で表された負の数の絶対値は、再度2の補数をとることで求めることができます。
したがって、
11000101
↓反転
00111010
↓1を加える
00111011
となり、解答はBとなります。