世界を支える数学～公開鍵暗号方式～

はじめに

私が大学生のころの話になります。ゼミの教授にからこんなことを問われました。「実生活の中で役立つ高等数学を見たことはあるか。」今の私たちの生活は数学が無ければ成り立たないものばかりで、簡単に答えられそうな質問です。当時の私も（何と答えたかは覚えていませんが）さらっと答えていたことを覚えています。しかしよく考えてみると、ほとんどの数学はその他の学問の裏方として活躍しているばかりで、純粋に数学が表舞台に立っているところはほとんど見かけません。
そんな縁の下の力持ちである数学が堂々と表舞台で活躍している姿を皆さんに知っていただきたいと思い、この記事を書きました。今回は、その中でも特に大活躍している「公開鍵暗号方式」について取り上げます。
本記事では、公開鍵暗号方式について記述する前に、公開鍵暗号方式誕生以前からある「共通鍵暗号方式」について記します。そこから公開鍵暗号方式が生まれた経緯を示し、最後に公開鍵暗号方式に使われている数学を紹介します。

共通鍵暗号方式とは

公開鍵暗号方式について記述する前に、昔から使われている共通鍵暗号方式について記述します。共通鍵暗号方式とは、簡単に言ってしまえば、ある平文（暗号化する前の文章）を暗号化する際に使う鍵と、暗号化された文章（暗号文）を復号（暗号文を平文に戻すこと）する際に使う鍵が共通である暗号化方式です。下の例を見てください。
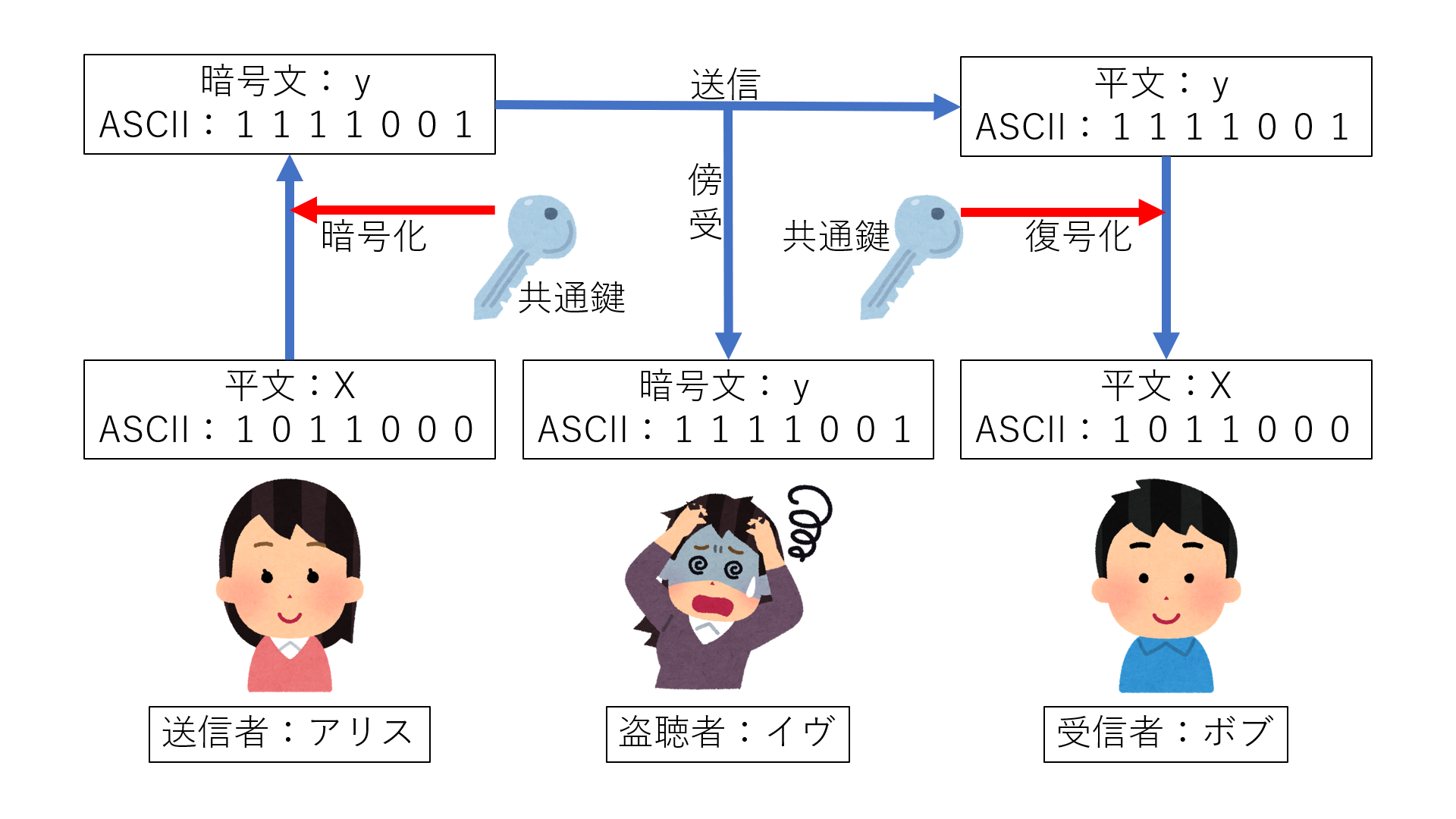
アリスがボブに「X」を送りたいとします。しかし２人の関係に嫉妬したイヴがアリスのメッセージを傍受しようとします。もちろんアリスは自分のメッセージを見られたくありません。そこでアリスはメッセージの暗号化を試みます。
暗号化の前にまずは「X」というメッセージをPCが理解するための形式であるASCIIに変換します。「X」をASCIIで表すと1011000。これを暗号化するときに必要となるのがアルゴリズム（暗号化に使う計算方式）と共通鍵です。今回のアルゴリズムを足し算、共通鍵を0100001とした場合、暗号化のための計算は、1011000＋0100001＝1111001となり、暗号文1111001が得られます。11110011はASCIIのコード表から「ｙ」となります。まとめると、「X」という平文を共通鍵で暗号化することによって暗号文「ｙ」が得られます。この暗号文をアリスはボブに送ります。例えイヴがこの暗号文を傍受したとしても鍵を手に入れない限りは平文の「X」を読み取ることはできません。
続いて、アリスからの暗号文を受け取ったボブは復号化をします。復号化の際には暗号化の作業の反対のことをします。「ｙ」のASCIIである1111001から、共通鍵である0100001を引きます。1111001－0100001＝1011000。1011000はASCIIコード表から「X」となります。これで２人はイヴに内容を知られることなくメッセージのやり取りができました。しかし、ここで１つ問題が発覚します。メッセージ送信者は共通鍵を取り決めた後に、その鍵をメッセージ受信者に届けなければならないのです。届ける方法はいくつかあります。まずは自分の足で受信者の元まで行き伝える方法。または絶対的な信用のある第３者に委託するという方法。他にもいくつか方法はありますが、どれも安全性や利便性において問題を抱えていました。

公開鍵暗号方式とは

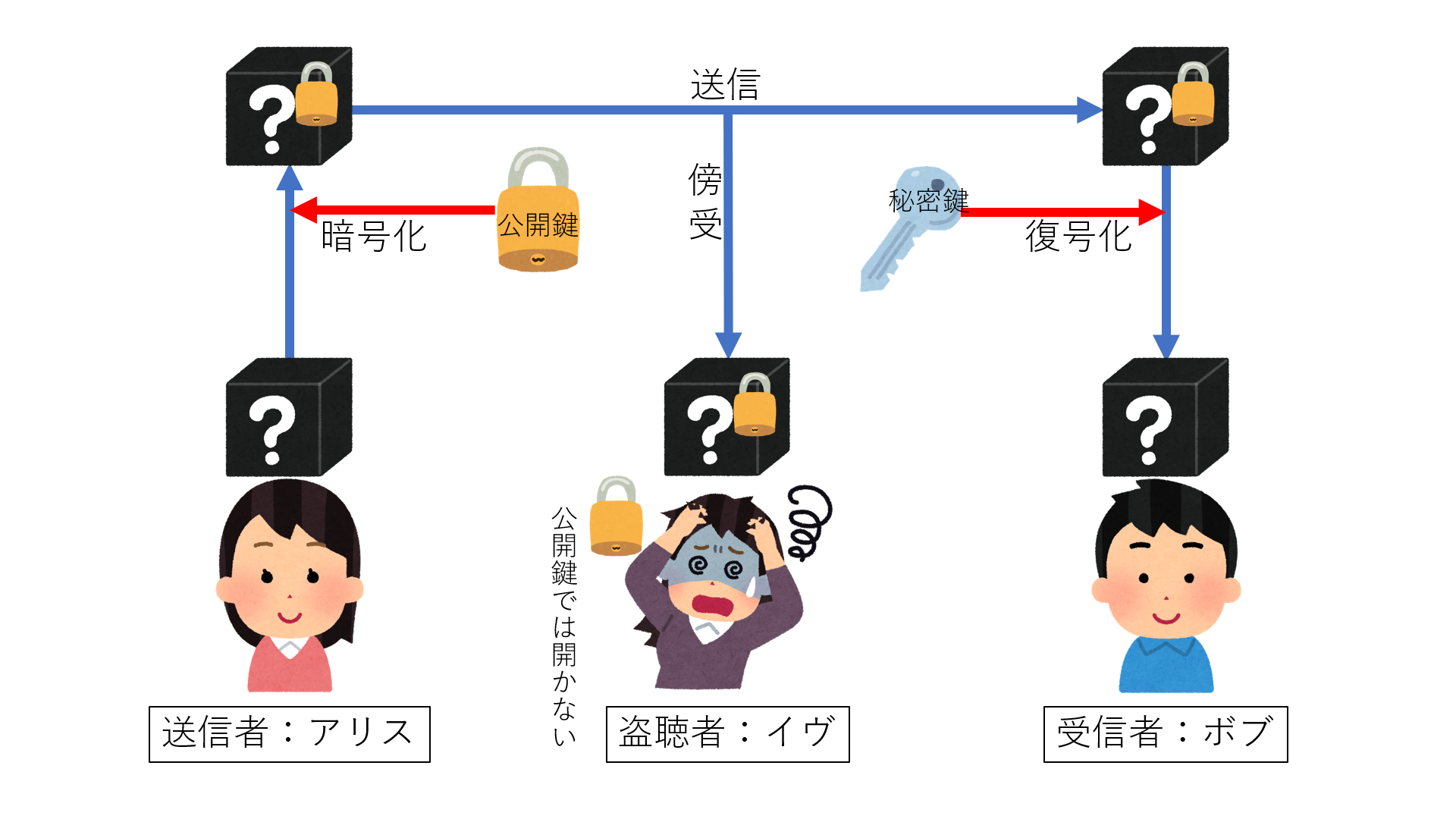
前項で共通鍵暗号方式の概要とその問題点を説明しました。共通鍵暗号方式での大きな問題として、メッセージ受信者と共通鍵を共有することが困難であるという点が挙げられました。この問題を解決したのが「公開鍵暗号方式」です。公開鍵暗号方式は、その名の通り、鍵作成者が、作成した鍵を全員に公開するという方式です。ただし、公開する鍵は２つの内１つだけです。公開する方の鍵を「公開鍵」公開しない方の鍵を「秘密鍵」といいます。それでは、実際にどのようにしてこの２種類の鍵を運用していくのか、再びアリス、ボブ、イヴのやり取りを見ていきましょう。
今回もアリスがボブに「X」というメッセージを送信します。共通鍵暗号方式と大きく変わるところは、メッセージの送信者ではなく受信者が鍵の作成者になることです。そこで受信者であるボブは公開鍵と秘密鍵を作成します。補足となりますが、公開鍵は南京錠、秘密鍵はそれを開けることができる鍵であるとイメージしていただけると理解しやすいかと思います。ボブは公開鍵（南京錠）を世界中の誰でも手にすることができるように公開します。そして今回はアリスがボブの公開鍵（鍵）を入手し、メッセージをその南京錠でロックして送信します。ボブの南京錠は誰でも手に入れることができますが、イヴが公開鍵（南京錠）を手に入れても公開鍵（南京錠）で公開鍵（南京錠）を開けることはできません。公開鍵を開けることができるのは秘密鍵を持っているボブしかいないのです。これで今回もイヴにメッセージの内容を読まれることなく、メッセージのやり取りができました。そして今回は、暗号化に使う鍵と復号化に使う鍵が異なっていることで、鍵を相手に送るということに神経をすり減らす必要がなくなりました。

通信の安全性を支える数学

それでは、本記事の本題である公開鍵暗号方式で使われている数式についてメッセージ送信者アリス・受信者ボブ・攻撃者（メッセージを傍受する人）イヴに再び登場してもらい、説明していきます。
① ボブは２つの素数pとqを選びます。本来であればpとqは十分に大きいものでなければなりませんが、今回は説明を簡単にするためにp＝11、q＝17とします。ボブはこれらの素数を秘密にしなければなりません。
② ボブは素数pとqを掛け合わせて数Nを得ます。N＝11×17。今回はN＝187となります。
③ さらにボブはもう1つの数eを選びます。このeは(p－1)×(q－1)と互いに素でなければなりません。(p－1)×(q－1)＝(11－1)×(17－1)＝160。今回はこの160と互いに素となる数eとしてe＝7とします。
④ ①、②、③で求めた数N＝187とe＝7が公開鍵となります。公開鍵となるこれら2つの数は全世界に公開しなければなりません。
⑤ 次はメッセージを数Mに変換します。メッセージの変換には共通鍵暗号方式でも取り扱ったASCIIを用います。今回取り扱うメッセージも前項同様「X」とします。「X」はASCIIに変換すると1011000。これを更に１０進数に変換すると88となります。よってメッセージ「X」を数値化したM＝88が得られます。
⑥ 下準備は整いました。いよいよ暗号化に入ります。メッセージ送信者のアリスは、まず公開鍵のリストの中から受信者であるボブの公開鍵であるN＝187とe＝7を得ます。
⑦ これら2つの鍵と、メッセージ「X」のを数値化したM=88を公開鍵暗号方式のアルゴリズムに当てはめます。そのアルゴリズムが「C＝M^e(modN)」です。この式に定数M、e、Nを代入するとC＝88^7(mod143)となります。
⑧ 次に得られた式を解いてCの値を得ます。

C＝88^7(mod187)＝{88^4(mod187)×88^2(mod187)×88^1(mod187)}(mod187)

88^1＝88≡88(mod187)

88^2＝7744≡77(mod187)

88^4＝59969536≡132(mod187)

88^7＝88^1×88^2×88^4≡88×77×132＝894432≡11(mod187)

こうしてアリスはC=11を得ました。このC＝11を暗号文としてボブに送信します。
この暗号文は平文をに対して「モジュラー計算」という規則性の見えないアルゴリズムを組み込んであるため、イヴこれを解読することは極めてです。
⑨ しかし正当な受信者であるボブは特殊な情報であるpとqを持っています。このpとqを用いてボブは暗号文の復号に使う秘密鍵dを求めます。dを求める式は以下の通りです。

e×d≡1{mod(p－1)×(q－1)}

7×d≡1(mod160)

d＝23

⑩ この秘密鍵dを用いて暗号文C＝11を復号します。復号に使う式は以下の通りです。

M＝C^d(modN)

M＝11^23(mod187)

M＝{11^1(mod187)×11^2(mod187)×11^4(mod187)×11^16(mod187)}(mod187)

M＝11×121×55×154≡88(mod187)

M＝88

求められたM＝88はASCIIコード表より「X」となり、無事に復号されました。
このようにしてアリスは公開鍵Nとe、ボブは秘密鍵dというように送信者と受信者が異なる鍵を持つ暗号方式が公開鍵暗号方式なのです。

おわりに

近年の情報化社会において、ネットワーク通信は私たちにとって必要不可欠なものとなっています。そのような社会において通信の安全性・信頼性は必要不可欠です。そしてそれらを保証しているのが今回ご紹介した高等数学の１つである「モジュラー計算」なのです。モジュラー計算のみならず、この世界には社会の根底を支える数学がたくさん隠れています。皆さんもぜひ探してみてください。