さくさく理解する Godot 入門（ただし2Dに限る）応用編ナンプレ（数独）基本問題自動生成【第1回】

はじめに

本稿では、「さくさくナンプレ」において、ナンプレ（数独）基本問題を自動生成するための使用したアルゴリズムについて、具体的なソースコードを示して詳しく解説する。

※ 「数独」は株式会社ニコリの登録商標です。

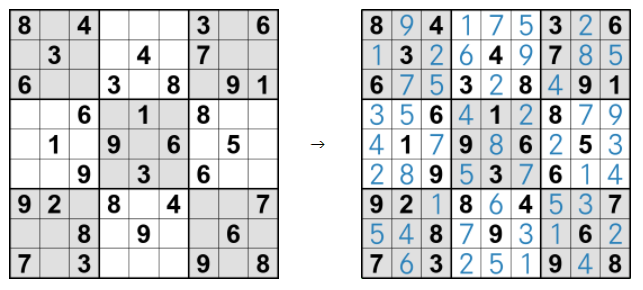
ナンプレは、9×9の盤面に、縦・横・3×3ブロック内で数字が重ならない（同じ数字が無い）ように、 1から9の数字を入れるパズルだ（下図参照）。より詳しいルール説明・具体例は wikipedia や「さくさくナンプレ」のページ参照のこと。

パズルのルールは法的に保護されていないが、パズル問題には著作権が存在する。
問題を自動生成するプログラムはAIの一種だと考えるが、AIが生成した問題コンテンツの権利が誰にあるのかは、現在議論中らしい。
だとしても、問題自動生成プログラムはビジネス的に価値があるものだ。本稿では、その価値ある秘密を惜しげもなく詳しく解説していくので、興味ある人は是非理解してなんらかの役にたててほしい。

ナンプレ問題を解く時に適当に数字を入れていくと、最終的に詰まってしまいにっちもさっちもいかなくなることが多い。それを避けるには、いろいろな解法テクニックを使って、確定する数字だけを入れていくとよい。
「さくさくナンプレ」で自動生成される問題は、初級解法テクニックのみで解ける基本問題のみだ。

ナンプレを解くための解法テクニックには、適用するのが簡単なものから難しいものまで多数のものが存在する。本稿における「初級解法テクニック」とは、候補数字（メモ）を使わなくとも適用できる解法テクニックのことで、具体的には以下の３つとする。

フルハウス
隠れたシングル
裸のシングル

各テクニックの説明は後述する。

なお、「さくさくナンプレ」の全ソースコードは github（https://github.com/vivisuke/NumberPlace）にあげている。 UI 部分のコードを読んでみたい、一部修正したいという人は是非参照してほしい。

問題自動生成アルゴリズム概要

本章では、問題自動生成アルゴリズム全体の大まかな流れを解説し、次章以降でそれぞれの処理について詳細に解説する。
細部の具体的な説明が本章にはないので、細部が気になって腑に落ちないかもしれないが、細部から先に説明すると、今度はなぜそのような処理が必要なのか、全体における位置づけがわからず理解が難しくなる。
よって、本章では細部にはこだわらず、全体の流れを理解するように努めてほしい。

問題自動生成は以下の手順で行う。

盤面（9×9）に解答パターン生成
盤面から数字をランダムにひとつ消す
盤面が問題として適切でなければ消した数字を戻す
まだ盤面から数字を消せるのであれば、2. から繰り返す
盤面の状態が自動生成された問題となっている

下図は生成した解答パターン例だ。

下図は解答パターンから数字をランダムに消していった例だ。

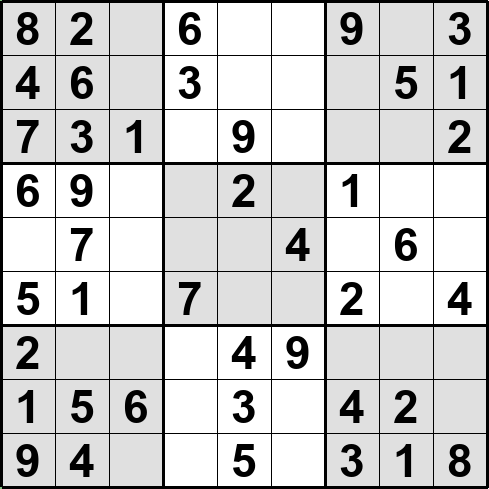
解答パターン生成は単純なバックトラッキングで高速に行うことができる。詳細は次章で説明する。
解答パターンが出来たら、そこから手がかり数字をできるだけ消していき、適切（proper）な問題かどうかをチェックする。
問題が適切な問題かどうかをチェックするアルゴリズムの詳細は後術する。

初中級問題では可能な限り数字を消すが、入門問題では空欄数が一定数に達したら数字を消す処理を修了する。

逆に、完全に空欄の盤面から始め、数字を置いていくというアルゴリズムも考えられるが、縦横ブロックで数字が重なっていないかをいちいちチェックする必要がある。
先に解答を生成し、数字を消していくアルゴリズムでは、消す処理時に数字の重なりチェックは不要だ。

このアルゴリズムは「貪欲（greedy）アルゴリズム」と呼ばれる

解答を作る、手がかり数字を消していく、適切な問題かどうかをチェックする、これらができればナンプレ問題を自動生成できるということを理解してほしい。
次章からそれぞれの処理の詳細について具体的に解説していく。

解答パターン生成(前半)

全セルについて再帰関数を使った単純なバックトラッキングを行うことで、解答パターンを簡単に生成することができる。バックトラッキングとは、一種の深さ優先探索で、可能な数字をどんどん試していき、行き詰まったら前に戻るというアルゴリズムだ。通常は再帰関数により実装される。
ただし、１行目は1から9の数字の順列（ランダムな順序に並べかえたもの）なので、要素が1から9の配列を作り、それをシャフルするだけでよい。
２行目からはセルに1～9の数字を入れていき、重なり（縦横ブロック内に同じ数字があること）があったら後戻りを行う。

重なりチェックはビット演算を利用するとかなり高速になる。
また、チェック時に関係するすべての場所との比較を行うより、あらかじめ配置可能なビットを計算しておいた方が高速になる。
この高速化テクニックは「N-Queens」でも使用したものだ。参照してほしい。

盤面のデータ構造としては数字をビットで表現した要素を持つ1次元配列（cell_bit）を用いる。
2次元配列の方が好きな読者もいるかもしれないが、たいていは1次元配列の方が高速で扱いやすい。
数字は1～9の数値でもよいのだが、数字をビットで表現しビット演算を行った方が遥かに高速になる。

解答パターンを生成するコードを以下に示す。

const N_VERT = 9
const N_HORZ = 9
const N_CELLS = N_HORZ * N_VERT
const BIT_1 = 0b0001    # 数字1に対応するビット
const BIT_2 = 0b0010    # 数字2に対応するビット
const BIT_3 = 0b0100
...
const BIT_9 = 0b100000000   # 数字9に対応するビット
const ALL_BITS = (1<<N_HORZ) - 1
var cell_bit = []           # 盤面を表す1次元配列、0 なら空、数字はビット（BIT_1, ... BIT_9）として表す
var column_used = []        # 各カラムの使用済みビット
var box_used = []           # 各3x3ブロックの使用済みビット
func gen_ans():     # 解答生成
    # 解答生成のためのもろもろの初期化処理
    column_used.resize(N_HORZ)      # 各列用
    box_used.resize(N_HORZ)         # 3x3ブロック用
    cell_bit.resize(N_CELLS)
    for i in range(column_used.size()): column_used[i] = 0    # 各列の使用済み数字ビット
    for i in range(box_used.size()): box_used[i] = 0    # 3x3ボックス内使用済み数字ビット
    for i in range(cell_bit.size()): cell_bit[i] = 0    # 各セルを空に
    var t = []      # １行目配列
    for i in range(N_HORZ): t.push_back(1<<i)     # 1～9 をビットに変換し格納
    t.shuffle()     # シャフル
    for i in range(N_HORZ):         # １行目について
        cell_bit[i] = t[i]          # 各セルの値設定
        column_used[i] = t[i]       # カラムごとの使用済みフラグ設定
        box_used[i/3] |= t[i]       # 3x3ブロックごとの使用済みフラグ設定
    gen_ans_sub(N_HORZ, 0)          # 解答生成再帰関数コール

もろもろの初期化処理を行った後に、バックトラッキングを行う再帰関数 gen_ans_sub(ix, line_used) をコールしている。