はじめに
について解説し、それらの処理速度比較を行う(Nクイーン問題の詳細は次章参照)。
言語は C++ を用いるが、テンプレートの黒魔術など難解な機能は使用していないので、
C#, Java などをマスターしている人にも充分読めるはずだ。
完全なソースコードは github に上げいるので、実際のコードを読みたい・試してみたい人は以下を参照してほしい。
github: https://github.com/vivisuke/NQueen
Nクイーン問題(N-Queens puzzle)
Nクイーン問題とは、NxNの盤面にチェスのクイーンN個を互いに効きが無い(クイーンは縦・横・斜め45度方向に効きがある)ように配置する問題だ。
一般的には8×8のチェス盤を用いる8クイーン問題が有名だが、本稿では盤面の縦横幅を8に固定せず、
NxNの盤面とし、現実的な処理時間(本稿では、処理時間が1秒を超えるまで盤面サイズをインクリメントしている)で、
どのサイズまでの解を求めることが出来るかに挑戦する。
Nクイーン問題は2×2、3×3盤面の場合は解が無いが、4×4以上は解が存在し、サイズが増えるに従って解の数が膨大になる。
下図に4×4の場合の唯一解を示す。縦横斜めに互いに効きが無いことを確認してほしい。

各行または各列には1個のクイーンしか置けないので、NxNの盤面におけるクイーンの最大値はN個である(N≧4の場合)。
Nクイーン問題は数独などの多くのパズル同様に制約充足問題に分類される。
なので、解を見つけるのは必ずしも容易ではないが、クイーンを配置した盤面が与えられると、
それが制約を満たすかどうかは容易に判定できる(盤面を縦横斜めから見て、重なりがなければOK)。
盤面が小さい場合は、単純な探索ですぐに解が見つかるが、盤面が大きくなると必要な探索空間が爆発し膨大な時間を要する。
世界記録は27×27(2016年)だが、それには膨大な計算機資源と高度なアルゴリズムが必要だ。
本稿では筆者所有の一般的なPCで、17×17までを解くことができる、それほどは高度ではないアルゴリズムを解説する。
力まかせ探索(Brute-force search)
まずは、もっとも単純な「力まかせ探索」から解説しよう。英語で言えば「Brute-force search」だ。
力まかせ探索は、全ての可能性のある解の候補を体系的に数えあげ、それぞれの解候補が問題の解となるかをチェックする方法だ。
パターン生成後にチェックするので「生成検査法(generate and test)」とも呼ばれる。
8クイーン問題の場合、8×8 = 64箇所に8個のクイーンを置く場合の数は、64 C 8 = 4.4*10^9にもなる。
が、各行には1個のクイーンしか置けない(同じ行に2つのクイーンを置くと、その時点でアウト)ので、8^8 = 16,777,216で充分だ。
したがって、力まかせ探索による Nクイーン問題の処理時間は O(N^N) となる。
以下、C++コードについて説明する。
まずは、配置済みクイーンが効き無しに置かれているかをチェックする関数 check() から。
int NQ は盤面サイズを表す。8クイーンなら8だ。
const char row[NQ] は、各行の何カラム目(1~NQ)にクイーンが配置されているかどうかを示す。
各行について、他の行と比べて、同じカラムに置かれてないか、斜め45度方向に置かれていないかをチェックし、
効きがあればその時点で false を返す。
効きがまったく無い場合は true を返す。つまり解を発見したということになる。
bool check(const char row[], int NQ) // 配置済みクイーンが効き無しに置かれているか?
{
for(int r = 1; r < NQ; ++r) { // 2行目から最後の行までチェック
for(int i = 0; i < r; ++i) { // r行と、最初~r-1行との効きチェック
if( row[i] == row[r] || abs(row[i] - row[r]) == r - i )
return false; // 水平 or 斜めに効きがある
}
}
return true;
}
次に、各行に順にクイーンを配置してチェックを行う関数を下記に示す。
C/C++ の配列は0から始まるので、n個を既に配置している場合、次は row[n] に配置することになる。
コードは単純で、for文で各行の何カラム目にクイーンを配置するかを決め、最後まで配置した場合は
check() を呼んで効きがあるかどうかをチェックし、なければ解を発見したとして解個数をインクリメントしている。
途中の場合は、配置した数をプラス1し、自分自身を再帰コールしている。
void generateAndCheck(char row[], int n, int NQ) // n: 配置済みクイーン数
{
for (row[n] = 1; row[n] <= NQ; ++row[n]) {
if (n == NQ - 1) { // 最後までクイーンを配置した場合
if (check(row, NQ)) // 効きチェック
++g_count; // 解を発見
}
else
generateAndCheck(row, n + 1, NQ);
}
}
以上で、コードを書き終わったので、あとは row 配列を宣言し、
generateAndCheck(row, 0, nq); とコールするだけだ。
これで全ての解を生成し、解個数をカウントできるわけだが、他のアルゴリズムに比べて処理速度はかなり遅い。
下記に筆者の環境で実行した場合の処理時間を示すが、9×9の時点で1秒を超えてしまった。
最近のCPUは数10年前に比べると恐ろしく高速で、
8クイーン問題程度であれば力ずくでもあっという間に探索を完了できるということだ。
処理時間測定結果:(Core i7-6700 3GHz, 32GB, Windows 10)
| N | 解の数 | BF(ミリ秒) |
|---|---|---|
| 4 | 2 | 0 |
| 5 | 10 | 0 |
| 6 | 4 | 0 |
| 7 | 40 | 6 |
| 8 | 92 | 90 |
| 9 | 352 | 2112 |
・力まかせ探索で10×10を解くと、どの程度の時間を要するかを予測しなさい
・対称形は解としてカウントしないように修正してみなさい
バックトラッキング探索(backtracking search)
力まかせ探索では最後までパターンを生成してから、チェックを行っていた。
だが下図のように1行目と2行目で既に互いに効きがある場合でも、それ以降の行にもクイーンを
置いてみてチェックする。これは明らかに時間の無駄である。

そこで、バックトラッキング探索では、パターンを生成し終わってからチェックを行うのではなく、
途中で制約を満たさないことが明らかな場合は、それ以降のパターン生成を行わないようにすることで、
処理時間の短縮を図る。これを枝刈り(pruning)と呼ぶ。
bool testNth(const char row[], int n) // row[0] から row[n] まで配置済み
{
for(int i = 0; i < n; ++i) {
if( row[i] == row[n] || abs(row[i] - row[n]) == n - i )
return false;
}
return true;
}
row[n] まで配置した時点で、効きがないかどうかをチェックするのが testNth() だ。
row[0] から row[n-1] までと row[n] を比較し、同一または斜め45度方向にクイーンが配置されていれば false を返し、
それらがひとつも無ければtrueを返す。
void backtracking(char row[], int n, int NQ) // n:配置済みクイーン数
{
for(row[n] = 1; row[n] <= NQ; ++row[n]) {
if( testNth(row, n) ) { // 制約を満たしている場合のみ先に進む
if( n + 1 == NQ )
++g_count; // 解を発見
else
backtracking(row, n+1, NQ);
}
}
}
backtracking() は上記のように testNth() を用いて記述できる。
力まかせ探索の generateAndCheck() とほぼ同じだが、最後まで配置してチェックするのではなく、
行にクイーンを置くたびに効きチェックを行って、効きがあればその状態からの探索を行わない点が異なる。
明らかに無駄な探索を行わないので、下記のように14×14でも4秒しかかからず、力まかせ探索と比べてはるかに高速になった。
処理時間は O(N!) 未満だ。
処理時間測定結果:(Core i7-6700 3GHz, 32GB, Windows 10)
| N | 解の数 | BF(ミリ秒) | BT(ミリ秒) |
|---|---|---|---|
| 4 | 2 | 0 | 0 |
| 5 | 10 | 0 | 0 |
| 6 | 4 | 0 | 0 |
| 7 | 40 | 6 | 0 |
| 8 | 92 | 90 | 0 |
| 9 | 352 | 2112 | 1 |
| 10 | 724 | N/A | 5 |
| 11 | 2680 | N/A | 21 |
| 12 | 14200 | N/A | 113 |
| 13 | 73712 | N/A | 671 |
| 14 | 365596 | N/A | 4158 |
制約テスト高速化(配置フラグ)
前章のバックトラッキング探索では、行の各カラムにクイーンを順に置いてみて、
各行に配置しているクイーンの位置と比較してクイーンの効きチェックを行っていた。
が、この処理はfor文で各行を調べていたので、意外と処理が重い。
しかもノードを探索するたびに呼ばれるので、トータルの処理回数が多くなり、それに時間を要する。
そこで、配置可能かどうかを表す配置フラグを事前に用意しておき、それを参照するだけで配置可能かどうかを判定することにする。
フラグをチェックするだけなのでfor文でチェックするよりはるかに高速だ。
チェックするときは高速になるかもしれないが、その配置フラグを更新するのに時間が必を要するのではないかと心配されるかもしれない。
しかし、Nクイーンの場合、各行の配置候補箇所はN箇所なので、N回効きチェックを行う必要があるが、
そのための配置フラグはそれ以前の状態で決まるので、更新は1回だけでよい。
つまり、配置フラグの方が処理回数自体が大幅に少なくなり、その結果高速になるということだ。
配置フラグとして、垂直・右上・右下方向についてクイーンを配置済みであることを表す
bool 型配列 col[], rup[], rdn[] を用意する(下図参照)。
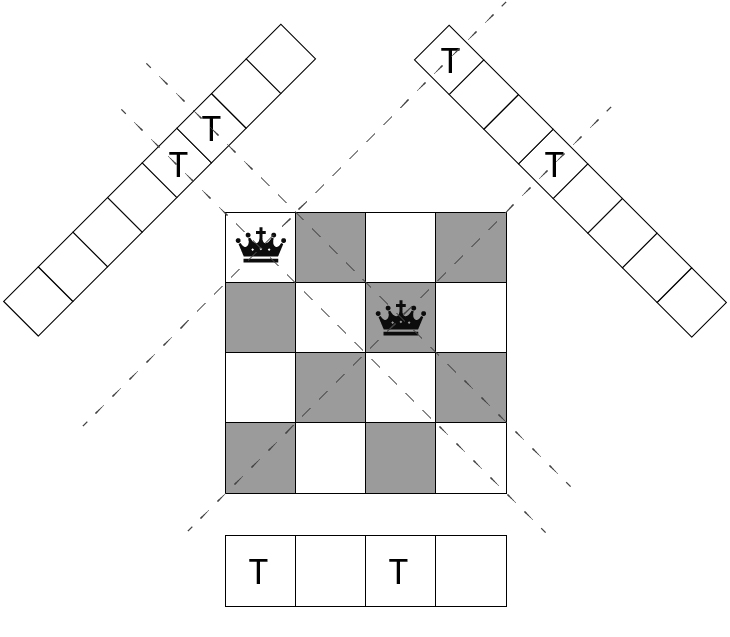
配置フラグを使用したプログラムは以下のようになる。
計算済みの配置フラグを引数で受け取り、フラグインデックスを計算し、
垂直・対角線方向にクイーンが配置済みかどうかをチェックし、どの方向にも配置済みでなければ、
そのカラムにクイーンを配置し、次の行に進むというわけだ。
void backtrackingFlags(
bool col[], bool rup[], bool rdn[], // 垂直・対角線方向配置済みフラグ
int n, int NQ) // n:配置済みクイーン数, [0, NQ)
{
for(int q = 0; q < NQ; ++q) {
const int uix = n + q; // 右上方向配置フラグインデックス
const int dix = q - n + NQ - 1; // 右下方向配置フラグインデックス
if( !col[q] && !rup[uix] && !rdn[dix] ) { // 垂直・右上・右下方向にクイーンを配置していない場合
if( n + 1 == NQ )
++g_count; // 解を発見
else {
col[q] = true; // 配置フラグセット
rup[uix] = true;
rdn[dix] = true;
backtrackingFlags(col, rup, rdn, n+1, NQ); // n+1個まで配置済みとして、自分自身を再帰コール
col[q] = false; // 配置フラグクリア
rup[uix] = false;
rdn[dix] = false;
}
}
}
}
配置フラグを使用した場合の処理時間計測結果を以下に示す。
処理時間オーダーは変わらないが、チェック時間が高速になった分処理時間が数倍短くなった
処理時間測定結果:(Core i7-6700 3GHz, 32GB, Windows 10)
| N | 解の数 | BF(ミリ秒) | BT(ミリ秒) | BT(ミリ秒) |
|---|---|---|---|---|
| 4 | 2 | 0 | 0 | 0 |
| 5 | 10 | 0 | 0 | 0 |
| 6 | 4 | 0 | 0 | 0 |
| 7 | 40 | 6 | 0 | 0 |
| 8 | 92 | 90 | 0 | 0 |
| 9 | 352 | 2112 | 1 | 1 |
| 10 | 724 | N/A | 5 | 8 |
| 11 | 2680 | N/A | 21 | 23 |
| 12 | 14200 | N/A | 113 | 50 |
| 13 | 73712 | N/A | 671 | 226 |
| 14 | 365596 | N/A | 4158 | 1361 |
関連記事
投稿が見つかりません。
 |
筆者:津田伸秀 プロフィール:テニス・オセロ・ボードゲーム・パズル類が趣味の年齢不詳のおじさん。 自宅研究員(主席)。vi と C++が好き。迷走中・・・ ボードゲーム・パズル系アプリ開発・リリースしてます。 |




