2020.11.02

Lv1

【Python独学】集合の比較と包含関係

kawashima

今回は、セット(集合)の比較と包含関係について、みていきましょう。

集合の要素の比較
集合の包含関係

集合の要素の比較

2つ以上の集合がある際、それぞれを比較することができます。
たとえば、2つの集合が持つ要素が等しいかどうか、共通する要素があるかどうか、などを比較して、
TrueかFalseを返すことができます。
以下の2つの方法についてみてみましょう。

・2つの集合の要素が等しいか比較する
・2つの集合に共通する要素があるか比較する

2つの集合の要素が等しいか比較する

2つの集合があるとき、それらが持つ要素が完全に一致しているかどうかを比較するには、
==演算子と!=演算子を用います。

==演算子は、2つの集合の要素が完全に一致していればTrue、1つでも異なればFalseを返します。
セット型は要素の順序を保持しないため、比較する集合の要素の順序は関係ありません。

!=演算子は、2つの集合の要素が一致しない場合にTrue、要素が完全に一致した場合にFalseを返します。

例をみてみましょう。

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

result1 = set_a == set_b     ### 2つの集合が完全に一致していればTrueを返す
result2 = set_a != set_b     ### 2つの集合が一致しない場合にTrueを返す

print(result1)
print(result2)

C:\Python> python 9-6_1.py
False
True

戻り値として真偽値（True、False）が返るため、if文の条件式に用いたりすることができます。

items = {"key", "jewel", "certificate"}
terms = {"key", "jewel", "certificate"}

if items == terms:
    print("必要なアイテムが揃っています!")
else:
    print("必要なアイテムが揃っていません")

C:\Python> python 9-6_2.py
必要なアイテムが揃っています!

2つの集合に共通する要素があるか比較する

2つの集合に共通する要素が1つでもあるか調べるには、isdisjointメソッドを用います。
一致する要素が全くなければTrueを返し、1つでもある場合はFalseを返します。

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

result = set_a.isdisjoint(set_b)     ### 共通する要素が1つ以上あるのでFalse

print(result)

C:\Python> python 9-6_3.py
False

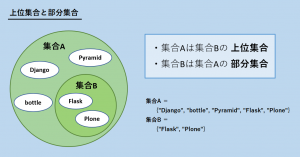
集合の包含関係

集合には、包含関係という2つの集合の要素の関係を表す言葉が定義されています。
それが、上位集合と部分集合です。

2つの集合があったとき、集合aが集合bの全ての要素を持っていた場合、
aはbの上位集合(スーパーセット)、bはaの部分集合(サブセット)と呼びます。

Pythonのセット型では、上位集合と部分集合を判定する演算子とメソッドが用意されています。
それぞれみていきましょう。

・aがbの上位集合かを判定する
・aがbの部分集合か判定する

aがbの上位集合か判定する

ある集合が他の集合の上位集合か判定する、つまり集合aが集合bの要素を全て持っているかどうかを判定する際は、
以下の3つの方法が用意されています。

・issupersetメソッド
・>=演算子
・>演算子

issupersetメソッドと<=演算子は、aがbの上位集合である場合、またはaとbの要素が一致している場合にTrueを返します。
また、>演算子は、aがbの上位集合である場合のみTrueを返します。

そして、>演算子がTrueである、つまりaがbの要素以外の要素も持っているような場合は、aはbの真上位集合とも呼びます。
メソッドと演算子の例をまとめてみてみましょう。

set_a = {"Plone", "Pyramid", "Django", "Flask", "bottle"}
set_b = {"Django", "Flask"}

result1 = set_a.issuperset(set_b)   ### aがbの上位集合であればTrueを返す
result2 = set_a >= set_b            ### 同上
result3 = set_a > set_b             ### 同上（完全に一致する場合を除く）

print(result1)
print(result2)
print(result3)

C:\Python> python 9-6_6.py
True
True
True

また、>演算子については以下の例のように、要素が完全に一致している場合はFalseを返します。

set_a = {"Django", "Flask"}
set_b = {"Django", "Flask"}

result = set_a > set_b

print(result)

C:\Python> python 9-6_7.py
False

aがbの部分集合かを判定する

ある集合が他の集合の部分集合である、つまり集合aの全ての要素を集合bが持っているかどうかを判定する際は、
以下の3つの方法が用意されています。

・issubsetメソッド
・<=演算子
・<演算子

こちらについては、基本的には部分集合の判定の逆だと思ってもらえればよいです。
issubsetメソッドと<=演算子は、aがbの部分集合である場合、またはaとbの要素が一致している場合にTrueを返します。
<演算子は、aがbの部分集合である場合のみTrueを返します。

真上位集合と同じように、<演算子がTrueである、つまりbがaの要素以外の要素も持っているような場合は、aはbの真部分集合とも呼びます。
例をみてみましょう。

set_a = {"Django", "Flask"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

result1 = set_a.issubset(set_b)   ### aがbの部分集合であればTrueを返す
result2 = set_a <= set_b          ### 同上
result3 = set_a < set_b           ### 同上（完全に一致する場合を除く）

print(result1)
print(result2)
print(result3)

C:\Python> python 9-6_4.py
True
True
True

上記のように、aの要素をbが持っているかどうかを判定するのに用いることができます。
また、<演算子については以下の例のように、要素が完全に一致している場合はFalseを返します。 [python] set_a = {"Django", "Flask"} set_b = {"Django", "Flask"} result = set_a < set_b print(result) [/python] [su_note note_color="#ffffff"] C:\Python> python 9-6_5.py
False
[/su_note]

まとめ

・集合の要素の比較には、==演算子と!=演算子、isdisjointメソッドを用いる
・部分集合、上位集合の判定には、issubsetメソッドとissupersetメソッド、<=演算子、<演算子、>=演算子、
　>演算子を用いる

確認問題

以下の文章の空欄を埋めてみましょう。

issupersetメソッドは集合Aが集合Bの〇〇〇〇であることを判定するのに用い、
issubsetメソッドは集合Aが集合Bの〇〇〇〇であることを判定するのに用いる。
また、>=演算子と>演算子、<=演算子と<演算子の違いは、2つの集合の要素が完全に一致している際の戻り値が異なり、>= / <= 演算子の場合は〇〇〇〇、> / < 演算子の場合は〇〇〇〇が返る。

答えはこちらの記事の最後に！
→3月掲載予定

前回の確認問題の回答例

前回の記事はこちら→【Python連載】集合演算子と演算メソッド

前回はこんな問題でした。

set_a = {“apple”, “banana”, “orange”, “kiwi”, “coconut”, “blueberry”, “muscat”}
set_b = {“kiwi”, “grape”, “lemon”, “cherry”, “papaya”, “plum”, “apple”}

1.上記の2つの集合から、和集合/積集合/差集合/対象差集合をそれぞれ取り出してみましょう。
その際、メソッドと演算子の2つの方法を使ってみましょう。

2.上記2つの集合から、和集合/積集合/差集合/対象差集合と取り出し、set_aの要素を更新しましょう。

以下にそれぞれの集合演算と、要素の更新の記述を載せておきます。

和集合

set_a = {"apple", "banana", "orange", "kiwi", "coconut", "blueberry", "muscat"}
set_b = {"kiwi", "grape", "lemon", "cherry", "papaya", "plum", "apple"}

set_c = set_a | set_b
set_d = set_a.union(set_b)
set_a.update(set_b)

print(set_c)
print(set_d)
print(set_a)

積集合

set_a = {"apple", "banana", "orange", "kiwi", "coconut", "blueberry", "muscat"}
set_b = {"kiwi", "grape", "lemon", "cherry", "papaya", "plum", "apple"}

set_c = set_a & set_b
set_d = set_a.intersection(set_b)
set_a.intersection_update(set_b)

print(set_c)
print(set_d)
print(set_a)

差集合

set_a = {"apple", "banana", "orange", "kiwi", "coconut", "blueberry", "muscat"}
set_b = {"kiwi", "grape", "lemon", "cherry", "papaya", "plum", "apple"}

set_c = set_a - set_b
set_d = set_a.difference(set_b)
set_a.difference_update(set_b)

print(set_c)
print(set_d)
print(set_a)

対象差集合

set_a = {"apple", "banana", "orange", "kiwi", "coconut", "blueberry", "muscat"}
set_b = {"kiwi", "grape", "lemon", "cherry", "papaya", "plum", "apple"}

set_c = set_a ^ set_b
set_d = set_a.symmetric_difference(set_b)
set_a.symmetric_difference_update(set_b)

print(set_c)
print(set_d)
print(set_a)