2020.11.02

Lv1

【Python独学】集合演算子と演算メソッド

今回は、セット(集合)の集合演算についてみていきます。

集合演算とは
4つの集合演算 -集合を作成する場合-
4つの集合演算 -集合を更新する場合-

集合演算とは

セット型を紹介した際にちらっと出てきましたが、セット型(集合)では、集合演算を扱うことができます。
集合演算とは、複数の集合が持つ要素を比較し、そこから新しい集合を作る演算です。
例えば、AとBの2つの集合が持つ要素の中で、共通した要素で新しい集合を作る、といった処理を
Pythonでは簡単に行うことができます。

例えば、複数の属性をセットで持つユーザー同士を比較して、共通する属性を取りあげたりする処理をメソッド1つで簡単に実現できます。

4つの集合演算 -集合を作成する場合-

集合演算には、以下の4つの演算が存在します。

・和集合
・積集合
・差集合
・対象差集合

それぞれの集合を新しく作成するための、メソッドと演算子が用意されています。
順番にみていきましょう。

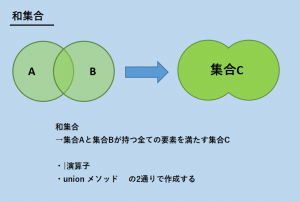
和集合の作成

複数の集合の要素を全て合わせた集合を和集合と呼びます。
和集合を求めるには、|演算子かunionメソッドを用います。
例をみてみましょう。

|演算子の場合

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

set_c = set_a | set_b            ### aとbの全ての要素を持つcを作成

print(set_c)

C:\Python> python 9-5_1.py
{‘Tornado’, ‘Pyramid’, ‘Django’, ‘bottle’, ‘Growler’, ‘Plone’, ‘Flask’}

unionメソッドの場合

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

set_c = set_a.union(set_b)        ### aとbの全ての要素を持つcを作成

print(set_c)

C:\Python> python 9-5_2.py
{‘Django’, ‘Tornado’, ‘Pyramid’, ‘Flask’, ‘Growler’, ‘bottle’, ‘Plone’}

上記の例のように、|演算子でもunionメソッドでも、複数の集合の全要素を持つ新しい集合を作成します。
どちらの方法も、2つだけではなく3つ以上の集合を扱うことができます。
|演算子の場合は、set_a | set_b | set_c …といった形で記述し、
unionメソッドの場合はカンマ区切りで複数の引数を与えます。

作成されるのはセット型のオブジェクトなので、要素は順番を持ちません。また、重複した要素は1つにまとめられます。

また、unionメソッド含めこのあと紹介する各種メソッドには、引数としてイテラブルなオブジェクトを与えます。
つまり、セット型だけでなくリストやタプルなども引数として扱うことができます。

set_a = {"Django", "Flask", "Growler", "Tornado"}
list_b = ["Plone", "Pyramid"]
tuple_c = ("Django", "Flask", "bottle")

set_d = set_a.union(list_b, tuple_c)        ### aとbとcの全ての要素を持つdを作成

print(set_d)

C:\Python> python 9-5_3.py
{‘Pyramid’, ‘Plone’, ‘Tornado’, ‘Growler’, ‘Django’, ‘bottle’, ‘Flask’}

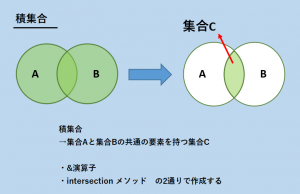
積集合の作成

複数の集合の共通部分のみを集めた集合を積集合と呼びます。
積集合を求めるには、&演算子かintersectionメソッドを用います。
例をみてみましょう。

&演算子の場合

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

set_c = set_a & set_b                    ### aとbの共通の要素を持つcを作成

print(set_c)

C:\Python> python 9-5_4.py
{‘Django’, ‘Flask’}

intersectionメソッドの場合

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

set_c = set_a.intersection(set_b)        ### aとbの共通の要素を持つcを作成

print(set_c)

C:\Python> python 9-5_5.py
{‘Django’, ‘Flask’}

2つの集合の中から共通する要素だけを取り出し、新しい集合を作成しています。
他の集合演算と同じように、複数の集合を扱うことができます。
intersectionメソッドはunionメソッドなどと同じように、集合以外のイテラブルなオブジェクトを引数として扱えます。

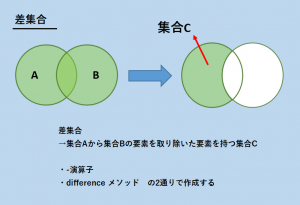
差集合の作成

ある集合から、別の集合の要素を取り除いた集合を差集合と呼びます。
差集合を求めるには、―演算子かdifferenceメソッドを用います。
例をみてみましょう。

-演算子の場合

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

set_c = set_a - set_b                    ### aからbの要素を取り除いたcを作成

print(set_c)

C:\Python> python 9-5_6.py
{‘Tornado’, ‘Growler’}

differenceメソッドの場合

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

set_c = set_a.difference(set_b)          ### aからbの要素を取り除いたcを作成

print(set_c)

C:\Python> python 9-5_7.py
{‘Growler’, ‘Tornado’}

aの要素から、bと共通する要素を取り除き、残った要素で新しい集合cを作成しています。
他の集合演算と同じように、複数の集合を扱うことができます。
differenceメソッドはunionメソッドなどと同じように、集合以外のイテラブルなオブジェクトを引数として扱えます。

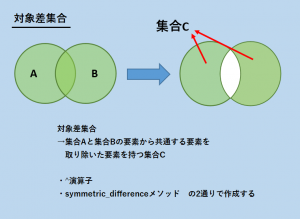
対象差集合の作成

複数の集合の中から共通する部分だけを取り除いた集合を対象差集合と呼びます。
対象差集合を求めるには、^演算子かsymmetric_differenceメソッドを用います。
例をみてみましょう。

^演算子の場合

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

set_c = set_a ^ set_b                      ### aとbの要素から共通する要素だけを取り除いたcを作成

print(set_c)

C:\Python> python 9-5_8.py
{‘Growler’, ‘bottle’, ‘Pyramid’, ‘Plone’, ‘Tornado’}

symmetric_differenceメソッドの場合

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

set_c = set_a.symmetric_difference(set_b)  ### aとbの要素から共通する要素だけを取り除いたcを作成

print(set_c)

C:\Python> python 9-5_9.py
{‘Growler’, ‘Tornado’}

aの要素とbの要素の中から共通する要素だけを取り除き、残った要素で新しい集合cを作成しています。
他の集合演算と同じように、複数の集合を扱うことができます。
symmetric_differenceメソッドはunionメソッドなどと同じように、集合以外のイテラブルなオブジェクトを引数として扱えます。

4つの集合演算-集合を更新する場合-

上記で確認した4つの演算子とメソッドは、それぞれ該当する集合を新しい集合として作成するものでした。
それに対して、新しい集合を作るのではなく、元になる集合の要素を更新するメソッドも用意されています。

和集合で更新

和集合で元となる集合を更新するには、updateメソッドを用います。

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

set_a.update(set_b)                     ### aとbの全ての要素でaを更新

print(set_a)

C:\Python> python 9-5_10.py
{‘Tornado’, ‘Pyramid’, ‘Flask’, ‘bottle’, ‘Django’, ‘Growler’, ‘Plone’}

上で紹介したunionで出来上がる集合と同じ要素が得られたかと思います。
unionと異なり、updateの場合は元になる集合aの要素をaとbの全ての要素で更新します。
なので、新しい集合は作られません。

積集合で更新

積集合で元となる集合を更新するには、intersection_updateメソッドを用います。

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

set_a.intersection_update(set_b)        ### aとbの共通の要素でaを更新

print(set_a)

C:\Python> python 9-5_11.py
{‘Flask’, ‘Django’}

上で紹介したintersectionで出来上がる集合と同じ要素が得られたかと思います。
intersectionと異なり、intersection_updateの場合は元になる集合aの要素と共通するbの要素でaの要素を更新します。
なので、新しい集合は作られません。

差集合で更新

差集合で元となる集合を更新するには、difference_updateメソッドを用います。

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

set_a.difference_update(set_b)          ### aからbの要素を取り除いた残りの要素でaを更新

print(set_a)

C:\Python> python 9-5_12.py
{‘Growler’, ‘Tornado’}

上で紹介したdifferenceで出来上がる集合と同じ要素が得られたかと思います。
differenceと異なり、difference_updateの場合は元になる集合aの要素をaからbの要素を取り除いた残りの要素で更新します。
なので、新しい集合は作られません。

対象差集合の更新

対象差集合で元となる集合を更新するには、symmetric_difference_updateメソッドを用います。

set_a = {"Django", "Flask", "Growler", "Tornado"}
set_b = {"Plone", "Pyramid", "Django", "Flask", "bottle"}

set_a.symmetric_difference_update(set_b)   ### aとbの要素から共通する要素を取り除いた残りの要素でaを更新

print(set_a)

C:\Python> python 9-5_13.py
{‘Pyramid’, ‘Growler’, ‘Plone’, ‘Tornado’, ‘bottle’}

上で紹介したsymmetric_differenceで出来上がる集合と同じ要素が得られたかと思います。
symmetric_differenceと異なり、symmetric_difference_updateの場合は元になる集合aとbの要素から、
共通する要素だけを取り除いた残りの要素でaの要素を更新します。
なので、新しい集合は作られません。

まとめ

・集合演算は、和集合/積集合/差集合/対象差集合の4種類
・それぞれの集合を作成する演算子及びメソッドが定義されている

演算子とメソッドについては、以下に表でまとめました。

集合演算	演算子	メソッド(作成)	メソッド(更新)
和集合	\|	union	update
積集合	&	intersection	intersection_update
差集合	–	difference	difference_update
対象差集合	^	symmetric_difference	symmetric_difference_update

確認問題

set_a = {“apple”, “banana”, “orange”, “kiwi”, “coconut”, “blueberry”, “muscat”}
set_b = {“kiwi”, “grape”, “lemon”, “cherry”, “papaya”, “plum”, “apple”}

1.上記の2つの集合から、和集合/積集合/差集合/対象差集合をそれぞれ取り出してみましょう。
その際、メソッドと演算子の2つの方法を使ってみましょう。

2.上記2つの集合から、和集合/積集合/差集合/対象差集合と取り出し、set_aの要素を更新しましょう。

答えはこちらの記事の最後に！
→【Python連載】集合の包含関係

前回の確認問題の回答例

前回の記事はこちら→【Python連載】セットの内包表記

前回はこんな問題でした。

以下のfor文を内包表記を用いて1文で記述してみましょう。

[python] set_num = set(range(10))
nums = set()

for i in set_num:
if i % 2 == 0:
nums.add(i**2)

print(nums)
[/python]

C:\Python> python 9-4_question.py
{0, 64, 4, 36, 16}

さて、この問題のfor文では、range(10)によって0～9までの値を要素として持つset_numに対して、
2で割り切れる要素は2乗して新しい集合numsに追加しています。
それを内包表記を用いて記述すると、以下のようになります。

nums = {i**2 for i in range(10) if i % 2 == 0}

print(nums)