問題自動生成（承前）
今回は除算問題自動生成について解説した後、
見た目の美しい問題を生成するアルゴリズムについて解説する。
除算問題自動生成
除算問題自動生成のアルゴリズムは乗算問題のそれと同じ流れだ。
ランダムに解答を生成し、できるだけ消去可能な数字を消去する。
数字を消去して、解が無い、または解が複数ある場合は消去不可とする。
商・除数・余りをランダムに生成すれば被除数・計算途中結果は自動的に決まるので、解答生成は簡単だ。
下記が除算問題を生成する genDiv() の定義。
商・除数・余りを引数で受け取り、被除数・計算途中結果を計算し、removeGreedyDiv() をコールして消去可能な数字を空欄にする。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | bool genDiv(std::vector<std::string>& vs0, std::vector<std::string>& vs, int A, // 商 int B, // 除数 int R, // 余り double p) // 残す数字割合{ if( !B ) return false; R %= B; // R >= B の場合対応 const auto astr = to_string(A); for(;;) { vs.clear(); // 文字列配列クリア vs.push_back(astr); // 商を最後に追加 vs.push_back(to_string(B)); // 除数を最後に追加 int C = A * B + R; // 被除数 vs.push_back(to_string(C)); // 被除数を最後に追加 int sc = 1; for (int i = 1; i != astr.size(); ++i) { // 商の桁数に合わせる sc *= 10; } for (int i = 0; i != astr.size(); ++i) { // 商の桁ごとに計算途中結果を生成 int t = astr[i] - '0'; // 商のi番目の桁 vs.push_back(to_string(B*t)); C -= B*t*sc; if( (sc /= 10) == 0 ) sc = 1; vs.push_back(to_string(C/sc)); } vs0 = vs; removeGreedyDiv(vs, p); // 貪欲法により、数字をできるだけ消す int cnt = count(vs[0].begin(), vs[0].end(), '*') + count(vs[1].begin(), vs[1].end(), '*'); if( cnt >= 2 ) return true; // 除数・商の空欄がひとつだけの場合はやり直し }} |
removeGreedyDiv() は、仮に数字を消し、isUniqDiv() をコールし、適切な問題かどうかをチェックし、
消去可能であればそれをリストに加える。
それらから一つをランダムに選び消去。これをできる限り行う。
ソースは removeGreedyMul() とほぼ同一なので、ここでは省略する。
具体的なコードを読みたい場合は github を参照していただきたい。
isUniqDiv() は問題がユニーク解を持つかどうかを判定する関数だ。基本的には除算問題ソルバーと同じ。
解を発見したら、カウンタをインクリメントし、2以上になったら探索を終了。
解の数が1であれば解がユニークなのでtrueを返す。これも isUniqMul() とほぼ同一なのでソースコードは省略する。
以下に genDiv() の使用例を示す。
なお、printDivQuest() は文字列配列を乗算問題として表示する関数で、
その定義は github のソースコードを参照されたい。
1 2 3 4 5 | std::vector<std::string> va0, va;if( genDiv(va0, va, g_mt() % 100, g_mt() % 100, g_mt() % 10, 0.0) ) { printDivQuest(va0); // 解答を表示（github 参照） printDivQuest(va); // 問題を表示（github 参照）} |
下記に本アルゴリズムで生成した2桁*2桁の除算問題を示す。
最初のものは p = 0.8 を、次のものは p = 0.0 を指定したものだ。
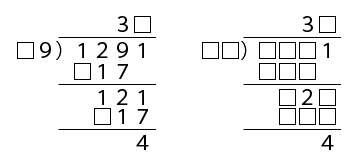
問題自動生成（改）
「数独」のオリジナルは「ナンバープレース（ナンプレ）」だが、ニコリ誌がそれを日本に紹介する時、
問題を対称形にし、見た目を美しくしたのが成功の一因と言われている。
つまり、見た目が美しくて解く意欲が出る問題自動生成には価値があるということだ。
そこで、虫食い算問題も見た目を美しくすると面白いのではないかと考えた。
何が、美しい問題かは難しいところだが、この章の最後に例をあげているように
手がかり数字を１種類だけ使う問題は美しく、解く意欲を喚起するのではないかと考えた。
１種類の手がかり数字だけを使う乗除算問題の生成は簡単で、解をランダムに生成した後、
特定の特定の数字以外を消し、それがユニーク解を持つ場合は、貪欲法でさらに消すだけだ。
乗算問題自動生成関数は以下のように定義できる
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | bool genMulOnly1( std::vector<std::string>& vs0, // 解答 std::vector<std::string>& vs, // 問題 int A, int B) // 被乗数・乗数{ vs.clear(); // 文字列配列クリア vs.push_back(to_string(A)); // 被乗数テキストを最後に追加 vs.push_back(to_string(B)); // 乗数テキストを最後に追加 int b2 = B; while( b2 ) { // 計算途中結果を乗数の桁ごとに計算 int t = b2 % 10; vs.push_back(to_string(A*t)); // 計算途中結果テキストを配列に追加 b2 /= 10; } vs.push_back(to_string(A*B)); // 乗算結果テキストを配列に追加 vs0 = vs; // 解を保存 for (char d = '1'; d <= '9'; ++d) { // d：残す数字 vs = vs0; for(auto& str: vs) { for(auto& ch: str) { if( ch != d ) ch = '*'; // d 以外の数字をすべて空欄に } } if( isUniqMul(vs) ) { // ユニーク解を持つ場合 removeGreedyMul(vs); // 可能ならさらに数字を消す int cnt = count(vs[0].begin(), vs[0].end(), '*') + count(vs[1].begin(), vs[1].end(), '*'); if( cnt != 0 ) // A*B に '*' が含まれる場合 return true; } } return false;} |
除算問題自動生成は、残す数字以外を消して isUniqDiv() をコールするだけで、
乗算問題とほぼ同じなので、コードは省略する（実際のコードは github 参照）。
生成できた問題例を以下に示しておく。
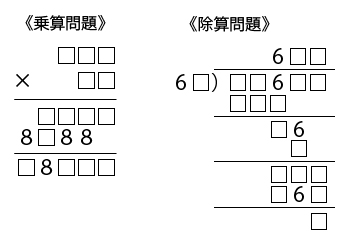
なかなか見栄えのいい問題が生成できるようになったのではないだろうか。
ちょっとしたアイデアで大きな成果が出た気分で、筆者としては大変満足している。
課題
・手がかり数字として ‘1’～’5′ をひとつづつだけ利用する乗除算問題を自動生成するプログラムを書いてみなさい。
・「SEND + MORE = MONEY」のように英単語を使った問題の自動生成に挑戦してみなさい。
おわりに
加乗除算虫食い算 ソルバー・問題自動生成アルゴリズムについて解説した。
最近のCPUは、単純な探索速度が人間に比べると極めて高速なので、一般人向け虫食い算であれば、
深さ優先探索を用いてほぼ解くことが可能だ。
解ランダム生成と貪欲法により一般人に解きごたえのある問題を生成することができる。
見た目の美しい問題を生成できれば、パズラーの解答欲をより刺激することができる（かもしれない）。
関連記事
投稿が見つかりません。
 |
筆者：津田伸秀 プロフィール：テニス・オセロ・ボードゲーム・パズル類が趣味の年齢不詳のおじさん。 自宅研究員（主席）。vi と C++が好き。迷走中・・・ ボードゲーム・パズル系アプリ開発・リリースしてます。 |
