承前
今回から2回にわたり、虫食い算を自動生成するアルゴリズムについて解説する。
虫食い算を解きたくて解きたくてしょうがないという人にはうってつけだ。
問題自動生成
一般的に、数独などの制約充足問題は、以下の手順で問題自動生成することができる。
1) 解をランダムに生成
2) 要素を消し解がユニーク(唯一)かどうかをチェック
3) 可能な限り 2) を繰り返す
可能な限り手がかりを消していくので、上記のアルゴリズムは「貪欲法(greedy algorithm)」と呼ばれる。
細かいことを言うと、消す順番によって、さらに多く消せる場合もあるのだが、
単純に消せるだけ消すアルゴリズムでも充分難しい問題を生成することができるパズルが多い。
問題自動生成では乱数を使用する。C++11 以降では mt19937(メルセンヌ・ツイスタ)という高性能な乱数生成器を利用できる。
以下のように記述しておくと、g_mt() で 0 から INT_MAX 未満の一様乱数を生成することができる。
#include <random> using namespace std; random_device g_rd; mt19937 g_mt(g_rd());
ある数(N)未満の乱数を生成したい場合は g_mt() % N と記述すればよい。
※ この記述では厳密には一様乱数にならないのだが、実用上は充分だ。
本稿の趣旨から外れるので、乱数に関する詳しい説明は行わないこととする。
詳しくは以下のページ等を見てね ;^p
http://vivi.dyndns.org/tech/cpp/random.html
加算問題自動生成
数独などのパズルでは解をランダムに生成することがそれなりに大変なのだが、
虫食い算の場合は、非常に簡単に解をランダムに生成することができる。
A + B + C = D の形式の加算問題であれば、A, B, C をランダムに生成すれば、
自動的にDが決まってしまうからだ。
また、加算の場合は同じ桁に複数の空欄があると解がユニークでなくなる
場合がほとんどなので、各桁の数字をどこかひとつ消せば問題が出来上がる。
下記が、各桁からひとつを選び空欄にする関数の定義
void removeAdd(vector<string> &vs) // 各桁から数字をひとつを選び空欄にする
{
int mxlen = 0; // 最大桁数
for(auto& txt: vs)
mxlen = max(mxlen, (int)txt.size());
int r;
for (int i = 0; i < mxlen; ++i) { // 下から何桁目の数字を空欄にするか
do {
r = g_mt() % vs.size(); // 何番目の数字を空欄にするか
} while ( i >= vs[r].size() ); // i番目の桁が無い場合は、やり直し
int ix = vs[r].size() - i - 1; // 先頭から ix 番目を空欄にする
vs[r][ix] = '*';
}
}
下記が、加算問題を生成する関数定義。加える数字は3つ(A, B, C)固定。
それらを引数として受け取る。
void genAdd(std::vector<std::string>& vs0, std::vector<std::string>& vs, int A, int B, int C)
{
vs.clear(); // 文字列配列クリア
vs.push_back(to_string(A)); // A を文字列に変換したものを、配列末尾に追加
vs.push_back(to_string(B));
vs.push_back(to_string(C));
vs.push_back(to_string(A+B+C));
vs0 = vs;
removeAdd(vs); // 各桁からひとつを選び空欄にする
}
実際に問題を生成する場合は、下記のようにA, B, C をランダムに生成し、
それらを引数に指定して genAdd() をコールするだけだ。
vector<std::string> vs0; // 解答を格納する文字列配列
vector<std::string> vs; // 問題を格納する文字列配列
genAdd(vs0, vs, g_mt() % 10000, g_mt() % 10000, g_mt() % 10000); // 問題自動生成
// 問題テキストは vs に格納されている
乗算問題自動生成
これまではボトムアップにアルゴリズムを解説してきたが、ここからはトップダウンに解説する。
どちらの方がわかりやすいだろうか?
乗算問題の解答ランダム生成も加算同様に簡単だ。被乗数・乗数のみを乱数で決めれば、計算途中結果、乗算結果が確定するからだ。
解答・問題テキスト、被乗数、乗数を引数に取り、この章の最初に説明した貪欲法により
問題を生成する関数 genMul() は以下のように定義できる。
被乗数に乗数の各桁の数字を掛けた計算途中結果と乗算結果を計算し、文字列配列に格納し、
removeGreedyMul() をコールし、貪欲法により数字を可能な限り消去する。
ただし、問題難易度指定のための p で残す数字の割合を指定可能としている。
// A*B を与えられ、貪欲法により問題を生成
bool genMul(std::vector<std::string>& vs0, std::vector<std::string>& vs, int A, int B,
double p = 0) // 残す数字割合
{
for (;;) {
vs.clear();
vs.push_back(to_string(A)); // 被乗数
vs.push_back(to_string(B)); // 乗数
int b2 = B;
while( b2 ) {
int t = b2 % 10;
vs.push_back(to_string(A*t)); // 計算途中結果
b2 /= 10;
}
vs.push_back(to_string(A*B)); // 乗算結果
vs0 = vs; // 解を vs0 に保存
removeGreedyMul(vs, p); // 貪欲法により可能な数字をできるだけ消す
int cnt = count(vs[0].begin(), vs[0].end(), '*') +
count(vs[1].begin(), vs[1].end(), '*');
if( cnt >= 2 ) return true; // 被乗数・乗数の空欄がひとつだけの場合はやり直し
}
}
以下は貪欲法により可能な数字をできるだけ消すremoveGreedyMul() の実装。
消しても問題がユニーク解を持つ数字位置を配列に入れ、乱数でどの数字を消すかを決定している。
これを消せなくなるまでか、残った数字が残すべき数字数より減るまで繰り返す。
// 貪欲法により可能な数字をできるだけ消す
void removeGreedyMul(vector<string> &vs,
double p = 0.0) // 残す数字割合、p が大きいほど数字が残る
{
// 最初に * に出来る位置の一覧を取得し、そこから * にしていく版
int cnt = 0;
for(const auto &s : vs)
cnt += s.size(); // 全文字数計算
int limit = round(cnt * p);
cnt -= limit; // cnt: 消すべき文字数
for (;;) {
vector<Pos> vpos; // 虫食いに出来る位置リスト
int row = 0; // 行位置
int col = 0; // 桁位置
for (;;) {
if( vs[row][col] == '\0' ) {
if( ++row == vs.size() ) // スキャン終わり
break;
col = 0;
continue;
}
auto ch = vs[row][col];
if( ch >= '0' && ch <= '9' ) {
vs[row][col] = '*'; // row, col の文字を空欄にし、
if( isUniqMul(vs) ) // それがユニーク解を持つかチェック
vpos.emplace_back(row, col);
vs[row][col] = ch;
}
++col;
}
if( vpos.empty() ) // 消せる数字が無くなった場合
break;
int r = g_mt() % vpos.size(); // 消す位置をランダムに決める
vs[vpos[r].m_row][vpos[r].m_col] = '*';
if( --cnt <= 0 ) break;
}
}
最後に問題がユニーク解を持つかどうかをチェックする isUniqMul()の定義を以下に示す。
ソルバー関数とほぼ同一だが、解を発見したら即終了ではなく、解個数をカウントし、2個以上になった場合は終了する。
// row行、col文字目の次から決めていく
// '*' を見つけた場合は '0' ~ '9' を順に入れて、再帰コール。ただし先頭桁に '0' は入らない
// '*' 以外はスキップ、A*B が確定した時点で解チェック
void isUniqMul(vector<string> &vs, int row, int col)
{
for (;;) {
auto ch = vs[row][++col];
if( ch == '*' ) {
for (ch = !col ? '1' : '0'; ch <= '9'; ++ch) {
vs[row][col] = ch;
isUniqMul(vs, row, col);
if( g_cnt > 1 ) // ユニークで無い場合
return;
}
vs[row][col] = '*';
return; // 当該行・桁の探索終了
}
if( ch >= '0' && ch <= '9' ) continue;
if( ch == '\0' ) {
if( ++row < 2 ) {
col = -1;
continue;
}
// A * B が確定した場合、解として成立しているかをチェック
if( checkMul(vs) ) {
++g_cnt; // 解として成立している場合は解数をチェック
}
return;
}
}
}
isUniqMul(const vector &vs0) は上記関数をコールし、解個数が1であれば true を、
そうでなければ(解無し or 解が2個以上)false を返す。
bool isUniqMul(const vector<string> &vs0)
{
g_cnt = 0;
vector<string> vs(vs0);
isUniqMul(vs, 0, -1);
return g_cnt == 1;
}
以下に genMul() の使用例を示す。
なお、printMulQuest() は文字列配列を乗算問題として表示する関数で、
その定義は github のソースコードを参照されたい。
std::vector<std::string> va0, va;
if( genMul(va0, va, g_mt() % 1000, g_mt() % 1000, 0.0) ) {
printMulQuest(va0); // 解答を表示(github 参照)
printMulQuest(va); // 問題を表示(github 参照)
}
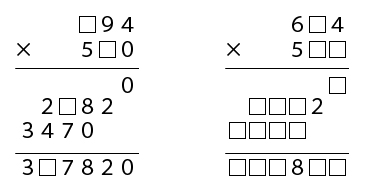
下記に本アルゴリズムで生成した3桁*3桁の乗算問題を示す。
最初のものは p = 0.8 を、次のものは p = 0.0 を指定したものだ。
関連記事
投稿が見つかりません。
 |
筆者:津田伸秀 プロフィール:テニス・オセロ・ボードゲーム・パズル類が趣味の年齢不詳のおじさん。 自宅研究員(主席)。vi と C++が好き。迷走中・・・ ボードゲーム・パズル系アプリ開発・リリースしてます。 |




