さくさく理解する Godot 入門（ただし2Dに限る）応用編テキサスホールデムポーカー【第5回】

期待勝率計算

AI の行動を選択するために、現在の手札・共有カードでの期待勝率を計算する。
期待勝率が高い場合は強気に行動（Raise, Call）し、低い場合は弱気な行動（Check, Fold）を選択するという戦術だ。

例えば下図は、プレイヤーBBの期待勝率を 84.85% と計算し（下部の「win rate[1] = 」の部分）、それがかなり高いので AI が強気になってレイズした状態だ（AIの手札が何なのかはわからないが、２，５，７いずれかのペアを持っているのかもしれない）。

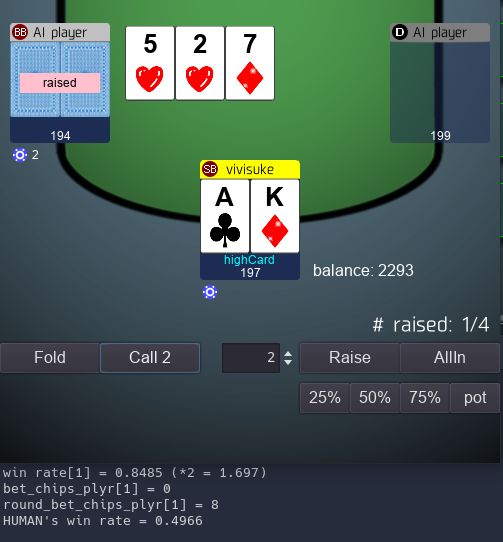
２枚の手札だけであれば、あらかじめ期待勝率を計算し公表しているサイトもあるが、共有カードも考慮した場合は、膨大な組み合わせ数になるので、事前に計算しておくことは実質不可能だ。

そこで、本アプリではモンテカルロ法を用いて、現在の手持ちカード、共有カードから期待勝率を計算する。
「モンテカルロ法」とは、乱数を発生させて何回も試行を行い、その結果により事象が発生する確率を予測するアルゴリズムだ。

手札、すでに配られた共有カードを用い、７枚に満たない場合は残りは未使用なカードをランダムに追加し、手役判定を行う。
さらに、参加人数分も同様に手役判定を行う。ただし、自分以外の手札は見えないので、その分も未使用カードをランダムに追加する。
そして、参加者全員よりも手役が上であれば勝利数を＋１する。そして勝利数を試行回数で割った値が期待勝率となる。

本アプリでの試行回数は5千回とした。試行回数が多いほど結果は正確になるが、その分計算時間が増大する。
実際に試してみて、5千回であれば、処理時間もそうかからず、十分な精度を得られたと判断したわけだ。

下記が、モンテカルロ法により期待勝率を計算する関数だ。

# モンテカルロ法による期待勝率計算、return [0.0, 1.0]
# 引数 nEnemy：降りていない敵プレイヤー数
func calc_win_rate(pix : int, nEnemy : int) -> float:
    var v = []      # v[0], v[1]：手札、v[2]～ コミュニティカード（無い場合もあり）
    v.push_back(players_card1[pix].get_sr())
    v.push_back(players_card2[pix].get_sr())
    for k in range(comu_cards.size()):
        v.push_back(comu_cards[k].get_sr())
    var wsum = 0.0
    var dk = []             # デッキ用配列
    dk.resize(N_CARDS)
    # 人間プレイヤーが降りた場合は、試行回数を減らし、処理を高速化
    var n_playout = N_PLAYOUT if !is_folded[HUMAN_IX] else N_PLAYOUT2
    for nt in range(n_playout):
        for i in range(N_CARDS):        # デッキ初期化
            var st : int = i / N_RANK
            var rank : int = i % N_RANK
            dk[i] = (st<<N_RANK_BITS) | rank
        for i in range(v.size()):   # v ですでに使用されているカードを外す
            var ix = card_to_suit(v[i]) * 13 + card_to_rank(v[i])
            dk[ix] = -1         # 使用済みフラグON
        # 自分の手札
        var u = v.duplicate()   # v を u にコピー
        while u.size() < 7:     # ７枚に満たない場合は、デッキからカードを追加
            u.push_back(get_unused_card(dk))
        var oh = check_hand(u)
        var nw = 1      # 勝者数
        var win = true
        for e in range(nEnemy):         # 降りていない敵プレイヤー数分ループ
            u[0] = get_unused_card(dk)      # 手札をランダムに決める
            u[1] = get_unused_card(dk)
            var eh = check_hand(u)          # 手役判定
            var r = compare(oh, eh)         # 手役判定
            if r < 0:
                win = false
                break       # 負けの場合
            if r == 0:          # 引き分けの場合
                nw += 1
        if win: wsum += 1.0 / nw
    return wsum / n_playout

引数には、プレイヤーインデックスと降りていない敵プレイヤー数が指定され、そのプレイヤーの期待勝率を返す。
各プレイヤーの手札は players_card1[pix], players_card2[pix] に格納されているので、それらを取り出し配列 v に格納する。また、共有カードのカードも取り出し v に追加しておく。
次に、デッキを作成し、すでに使用済みカードを取り除く。そして、共有カードが５枚に満たない場合はデッキから未使用カードをランダムに取り出し、配列 v に追加する（ランダムに取り出すのではなく、デッキをシャフルしておいてもいいのだが、シャフルの方が処理時間を要するので、このようにした）。これで７枚そろったので、前章で説明した check_hand() を呼び出し、手役判定を行い結果を保存しておく。
次に降りていない敵の数だけ、同様の処理を行う。ただし、敵の手札が何なのかはわからない（AI はズルしない）ので、手札もランダムに選び手役判定を行う。そして引数で指定されたインデックスのプレイヤーの手役と比較し、敵が勝っていれば負けとする。勝っていた場合はループを継続し、他の敵全員と同様の処理を行う。
敵全員に勝っていた場合は、勝利数をインクリメントする。
そして最後に勝利数をプレイアウト数で割った値を期待勝率として返している。

下記は、未使用カードひとつをランダムに取得し、そのカードを使用済みにする get_unused_card() のコードだ。

func get_unused_card(dk):   # 未使用カードをひとつゲット、そのカードは使用済みに
    var ix
    while true:
        ix = rng.randi_range(0, N_CARDS-1)
        if dk[ix] >= 0: break   # 未使用カードの場合
    var cd = dk[ix]
    dk[ix] = -1     # 使用済みフラグON
    return cd       # 取り出したカードを返す

以下は、ランクも考慮した手役比較を行う compare(hand1, hand2) のコードだ。

# ランクも考慮した手役比較
# return: -1 for hand1 < hand2, +1 for hand1 > hand2
func compare(hand1 : Array, hand2 : Array):
    for i in range(hand1.size()):
        if hand1[i] < hand2[i]: return -1       # hand2 が勝っている場合
        elif hand1[i] > hand2[i]: return 1      # hand1 が勝っている場合
    return 0        # 引き分け

手役判定結果は配列で返され、最初に手役番号（大きいほど強い）、ついで、手役が同じ場合でも強弱を判定するカードランクが順に格納されている。なので、配列の先頭から順に比較していき、不一致になった時点で結果（-1 or +1）を返している。最後まで同じだった場合は引き分けとして 0 を返している。