目次
- ヘックス迷路脱出
- 概要
- 画面作成
- 初期化処理
- フレームごとの処理
- 学習結果
ヘックス迷路脱出
■概要
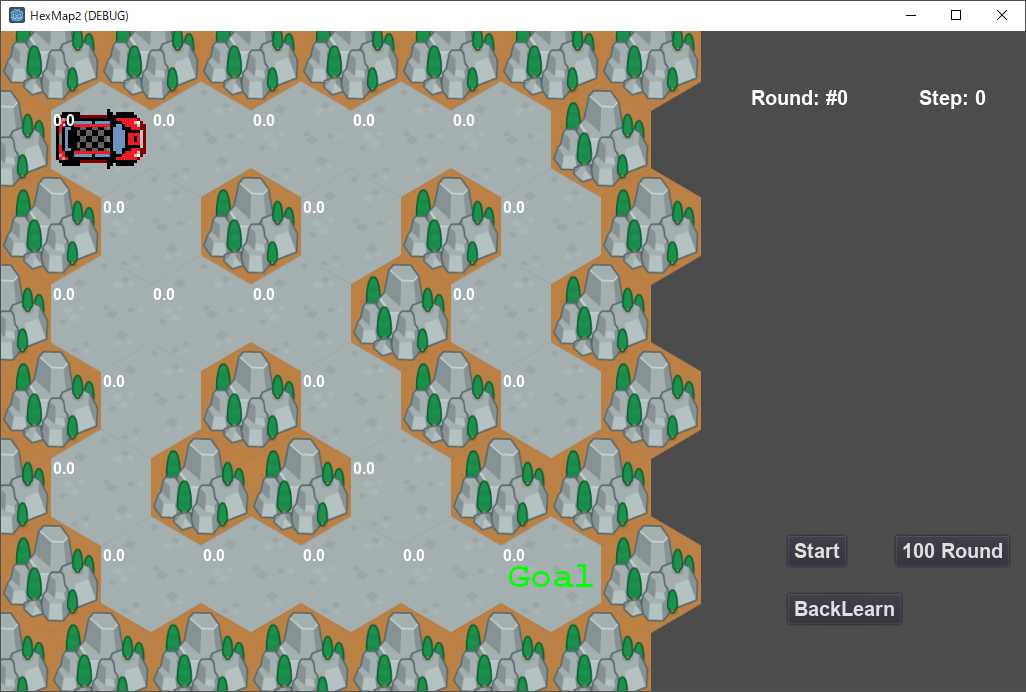
本章では上図のように、ヘックス(六角形)マップの迷路に車のエージェントを配置し、 スタートからゴールまでの経路を学習するコードを解説する。
マップをヘックスにしたのは、車の進行方向を60度単位としたためだ。 前章の迷路脱出では、エージェントは自由に上下左右に移動可能だったが、今回は車の向いている方向にしか前進できないものとする。 ただし直進だけでは迷路を脱出することは不可能なので、左右にハンドルを切ることができるものとする。 左にハンドルを切った場合は、進行方向に1マス移動したあとに車が左に60度ターンする。右ハンドルであれば右に60度ターンする。 また、行き止まりに突き当たっても元に戻れるように、バックの場合は先に車をターンしてから後退するものとする。
前章の迷路では、エージェントの位置だけが状態であったが、 本章ではそれに加えて車が向いている方向(6種類)も状態に加わることになり、Q値テーブルがその分大きくなり、 学習もより時間が必要となってくる。
いつものように、この迷路脱出プロジェクトは github(https://github.com/vivisuke/HexMap2)にあげているので、 ぜひダウンロードし、実際に動かしたり、パラメータを変更したりして試してほしい。
■画面作成
ゼロからヘックスマップを実装するのはいろいろ大変だが、Godot の TileMap はヘックスマップ用の設定が用意されており、 実装が楽ちんだ。
TileMap をヘックスマップにするには、インスペクターで Cell > HalfOffset を「Offset X」に設定するだけだ(下図参照)。
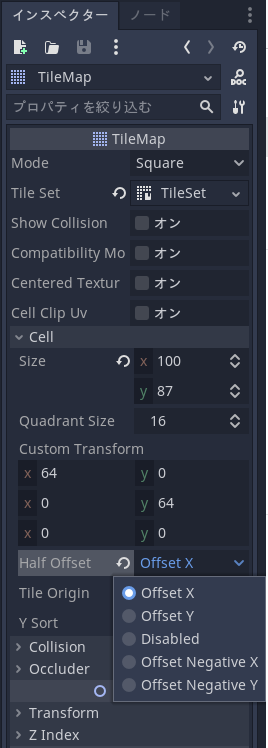
最初、Mode にヘックスがないのではてな?と思ったが、X 方向を1行ごとに半分ずらすという設定があった。
設定には「Offset Y」というものもあり、これはY方向を1列ごとに半分ずらすという設定だ。 本アプリでは「Offset X」を選択している。 これで1行ごとにセル表示位置が正の方向に半分ずれるのだが、「Offset Negatine X」「Offset Negatine Y」を選べば、 表示が負の方向に半分ずれる。
あとは、ヘックスマップ用の地形画像を用意して、タイルセットに登録するだけだ。
なお、キャラクタ・背景画像は、前章同様 kenney様(https://www.kenney.nl/)のものをありがたく使用させていただいている。
以上で、エディタの表示が下図のようになり、ヘックスマップを自由に編集可能となる。

■初期化処理
初期化処理のコードを下記に示す。
func _ready():
rng.randomize() # 乱数ジェネレータシードランダム化
TileMapGPos = $TileMap.global_position # タイルマップ原点位置
qLabel.resize(N_HORZ*N_VERT) # ラベル配列サイズ指定
init_Q_table() # Q値テーブル初期化
for y in range(N_VERT): # 全マップについてループ
for x in range(N_HORZ):
if $TileMap.get_cell(x, y) < TILE_WALL: # (x, y) が床の場合
var gpos = $TileMap.map_to_world(Vector2(x, y)) + TileMapGPos + Vector2(2, 30)
var label = QValueLabel.instance() # ラベルインスタンス生成
label.rect_position = gpos # ラベル位置設定
add_child(label) # 画面に配置
qLabel[xyToIX(x, y)] = label # ラベル配列に登録
if $TileMap.get_cell(x, y) == TILE_GOAL: # (x, y) がゴールの場合
GOAL_XY = Vector2(x, y) # ゴール位置保存
$Car.position = xyToCenterPos(START_XY) # 車スタート位置設定
配列サイズを設定し、init_Q_table() をコールしてQ値テーブルの初期化を行い、 盤面の各セルについて、そこが床であればQ値表示のためのラベルインスタンスを生成・設置し、 ゴール地点であればその位置を保存している。
下記は、Q値テーブル初期化を行う init_Q_table() の実装だ。
func init_Q_table():
Q.resize(QTABLE_SIZE)
# for i in range(Q.size()): Q[i] = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, ]
for i in range(Q.size()): Q[i] = [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, ] # 楽観的初期値
var ix = 0
for y in range(N_VERT):
for x in range(N_HORZ):
var pos = xyToCenterPos(Vector2(x, y))
for deg in range(0, 360, 60): #
for act in range(N_ACT):
var to = get_dstPosPDA(pos, deg, act) # 移動先位置を返す
if to.x < 0: Q[ix][act] = -1 # 移動不可の場合
ix += 1
このヘックス迷路脱出では、学習が局所最適値に陥ることを防ぐために ε-greedy 法は用いず、 楽観的初期値法を用いる。
楽観的初期値法とは、行動可能なQ値の初期値すべてを最大値にしておくことで、 ゴールに到達する経路が見つかっても、そのQ値はすぐには最大値にはならないで、 まだ試していない行動があればそれを全部試してみる、というアルゴリズムだ。 すべての経路を探索するので、学習に時間はかかるが、状態数が膨大でなければ最適経路を見つけられる確実な方法だ。
というわけで、各行動の初期Q値を最大値(本稿では +1.0)に設定し、各セルについて、移動不可能な行動があれば、 そのQ値を最小値(-1.0)に設定している。
func get_dstPosPDA(pos, deg, act) -> Vector2 : # 移動不可の場合は (-1, -1) を返す
if act == ACT_BL: deg += 60 # 左後退の場合は先に車の進行方向を変更
elif act == ACT_BR: deg -= 60 # 右後退の場合は先に車の進行方向を変更
var rad = deg * PI / 180
var dp = Vector2(cos(rad)*CELL_WIDTH, sin(rad)*CELL_HEIGHT) # 移動方向
if act >= ACT_BW: dp = -dp # 後退の場合は、移動方向反転
var to = pos + dp # 移動処理
var m = $TileMap.world_to_map(to - TileMapGPos)
to = $TileMap.map_to_world(m) + TileMapGPos + MAP_CENTER
if $TileMap.get_cellv(m) == TILE_WALL:
return Vector2(-1, -1) # 移動不可
else:
return to
上記はアクション(act)が行動可能かどうかを判定する関数の実装。
アクションに従って、車の向きを変え、移動してみてそこが壁でないならば移動可能箇所を、移動不可ならば (-1, -1) を返す。
■フレームごとの処理
下記にフレームごとの処理コードを示す。
func _process(delta):
....
var act = -1
#if rng.randf_range(0, 1) <= 0.99:
if true: # 楽観的初期値の場合
act = sel_act_maxQ(qix0) # 最大Q値のアクションを選択
else: # ε-greedy の場合
act = sel_act_random() # 行動をランダムに選択
if act < 0: # 行動不能の場合
started = false
else:
doAction(act) # アクションを実行
var xy = get_carMapXY() # 車位置
var qix = xyaToQIX(xy, $Car.rotation_degrees / 60) # Q値テーブルインデックス
var reward = 0.0 # 報酬
var maxQ = 0.0 # 最大Q値
if is_goaled(xy, $Car.rotation_degrees): # ゴール位置の場合
started = false
reward = REWARD_GOAL
else:
maxQ = Q[qix].max() # 最大値取得
Q[qix0][act] += ALPHA * (reward + GAMMA * maxQ - Q[qix0][act]) # Q値更新
....
処理内容は前章の迷路脱出とあまり変わらない。
大きく違うのは、こちらは ε-greedy を使わず、楽観的初期値法を使っているので、 乱数によりランダムウォークをする必要が無いという点だ。
後述する sel_act_maxQ(qix) で最大Q値を与えるアクションを取得し、それを実行し、 Q学習の式に従ってQ値テーブルを更新している。
sel_act_maxQ(qix) の実装を下記に示す。
func sel_act_maxQ(qix):
var maxQ = -99
var lst = []
for act in range(N_ACT):
var dst = get_dstPos(act) # 移動先位置取得
if dst.x >= 0:
if Q[qix][act] > maxQ:
maxQ = Q[qix][act]
lst = [act]
elif Q[qix][act] == maxQ:
lst.push_back(act)
if lst.empty(): return -1
if lst.size() == 1:
return lst[0]
return lst[rng.randi_range(0, lst.size()-1)]
指定場所において、すべてのアクションを試し、実行可能であれば、現最大値と比べ、大きければそのアクションをリストに保存する。 現最大値と同じであれば、リストに追加する。全アクションを試したあと、リスト内のアクションが一つだけであればそれ(リスト先頭)を、 複数あれば乱数で選んだアクションを返す。
アクションを実行する doAction(act), get_dstPos(act) のコードを下記に示す。
func doAction(act):
var to = get_dstPos(act) # 移動先位置取得
if to.x >= 0:
$Car.position = to
if act == ACT_FL || act == ACT_BR:
$Car.rotation_degrees -= ROT_ANGLE
if $Car.rotation_degrees < 0: $Car.rotation_degrees += 360
elif act == ACT_FR || act == ACT_BL:
$Car.rotation_degrees += ROT_ANGLE
if $Car.rotation_degrees >= 360: $Car.rotation_degrees -= 360
func get_dstPos(act) -> Vector2 : # 移動不可の場合は (-1, -1) を返す
return get_dstPosPDA($Car.position, $Car.rotation_degrees, act)
get_dstPos(act) で移動先位置を取得し、車オブジェクトの位置を更新する。 また、左右にハンドル切った場合は、車オブジェクトの角度を更新している。 このとき角度が [0, 360) の範囲になるように修正している。
get_dstPos(act) のコードは単純で、車オブジェクトの位置、角度を実引数にして get_dstPosPDA() をコールしているだけだ。
■学習結果
下図に100ラウンド学習した結果を示す。
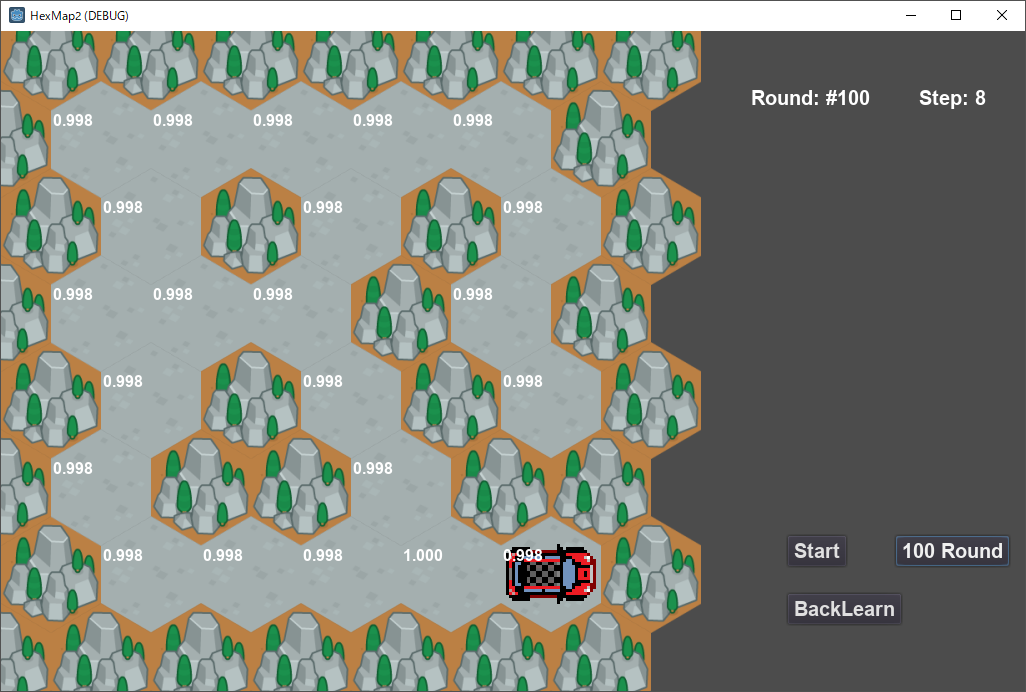
また、下図にはゴールまで到達するのに要したステップ数の10ラウンドごとの平均を示す。 100ラウンドだけでは、最短経路(8ステップ)を発見するまでには至っていないが、 徐々に平均ステップ数が減少しており、学習が進んでいることが確認できる。
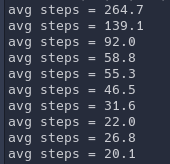
Q値テーブルが大きくなってくると、それを表示することも困難だし、 たとえ表示しても学習がちゃんと進んでいるのかどうかを確認するのが困難だ。
なので、このようになんらかの学習進捗指標を表示すると、徐々に学習が進んでいることがわかる。
本稿では学習がうまくいった場合しか示していないが、ソースコードを修正したり、パラメータを変更したりすると、 学習が期待したよう進まなくなってしまったり、局所最適解から抜け出せなくなったりすることがある。 そのようなときは、このようにして学習進捗の状態を確認して、対策するのが肝要だ。
TechProjin Godot入門 関連連載リンク
Godotで学ぶゲーム制作
さくさく理解するGodot入門 連載目次
標準C++ライブラリの活用でコーディング力UP!
「競技プログラミング風」標準C++ライブラリ 連載目次




