目次
- ロジカルに解けるかのチェック(後半)
- 貪欲法
- 対称形問題生成
- おわりに
ロジカルに解けるかのチェック(後半)
これまでに示した「フルハウス」、「隠れたシングル」、「裸のシングル」 のいずれかを探し、発見した場合はその数字を盤面に入れ、候補数字配列を更新する step_solve() のコードを以下に示す。
func step_solve() -> bool:
var pb = search_fullhouse()
if pb != []: # フルハウス発見
cell_bit[pb[0]] = pb[1] # セルに数字を入れる
update_candidates(pb[0], pb[1]) # 候補数字配列更新
return true
pb = search_hidden_single()
if pb != []: # 隠れたシングル発見
cell_bit[pb[IX_POS]] = pb[IX_BIT] # セルに数字を入れる
update_candidates(pb[IX_POS], pb[IX_BIT]) # 候補数字配列更新
return true
#if g.qLevel < OPT_NORMAL: return 0
pb = search_nakid_single()
if pb != []: # 裸のシングル発見
cell_bit[pb[IX_POS]] = pb[IX_BIT] # セルに数字を入れる
update_candidates(pb[IX_POS], pb[IX_BIT]) # 候補数字配列更新
return true
return false
search_fullhouse() 等を順に呼び、それらを適用できる箇所を発見した場合は、 数字を入れ、update_candidates(ix, b) を呼んで次の処理のために候補数字を更新している。
下記に、盤面の ix 位置に数字ビット b を入れたときに、候補数字配列を更新する update_candidates(ix, b) のコードを示す。
func update_candidates(ix : int, b : int): # ix に b を入れたときの候補数字更新
candidates_bit[ix] = 0
var x = ix % N_HORZ
var y = ix / N_HORZ
for t in range(N_HORZ):
candidates_bit[xyToIX(t, y)] &= ~b
candidates_bit[xyToIX(x, t)] &= ~b
var x0 = x - x % 3 # 3x3ブロック左上位置
var y0 = y - y % 3
for v in range(3):
for h in range(3):
candidates_bit[xyToIX(x0 + h, y0 + v)] &= ~b
処理は単純で、ix に関係する位置の候補数字の b ビットを0にしまくっているだけだ。
以上で準備が整ったので、ロジカルに解けるかをチェックする関数 can_solve() のコードを以下に示す。
func can_solve():
var sv = cell_bit.duplicate() # 盤面を保存
init_candidates() # 候補数字初期化
while true:
if !step_solve(): break # 初級解法テクニックを適用
var f = is_filled()
cell_bit = sv # 盤面を元に戻す
return f
func is_filled(): # セルが全部埋まっているか?
for i in range(cell_bit.size()):
if cell_bit[i] == 0: return false # 空欄が残っている場合
return true
すべての準備が整っていれば、あとは簡単だ。step_solve() を繰り返し呼んで、 最後に盤面がすべて埋まっているかどうかをチェックするとよい。
以上で、仮定法を使わず、初級解法テクニックだけを使ってロジカル(人間的) に解ける問題かどうかをチェックすることができるようになったわけだ。
貪欲法
貪欲法のコードは以下の通り
var rmix_list = [] # 削除位置配列
func gen_quest_greedy():
gen_ans() # 解答生成
for ix in range(N_CELLS):
rmix_list.push_back(ix) # すべての位置を rmix_list に追加
rmix_list.shuffle() # 順番をランダムにするためにシャフル
rmixix = 0 # 次に削除する位置
削除する箇所を rmix_list に入れ、次に削除する位置を rmixix に入れているだけだ。 実際に数字を消す処理は、各フレームごとに呼び出される下記の _proxess(delta) で行われる。
func _process(delta):
.....
if !rmix_list.empty(): # 問題自動生成中
var sv = cell_bit.duplicate() # 現在の状態を保存
var x = rmix_list[rmixix] % N_HORZ
var y = rmix_list[rmixix] / N_HORZ
var lst = []
lst.push_back(xyToIX(x, y)) # 削除位置をリストに追加
if symmetric:
lst.push_back(xyToIX(y, x))
lst.push_back(xyToIX(N_HORZ - 1 - x, N_VERT - 1 - y))
lst.push_back(xyToIX(N_VERT - 1 - y, N_HORZ - 1 - x))
for i in range(lst.size()):
cell_bit[lst[i]] = 0 # 数字削除
if !can_solve(): # 解がない or 解が複数ある
cell_bit = sv # 削除した数字を元に戻す
else:
nRemoved += 1
print("can solve, nRemoved = ", nRemoved)
rmixix += 1 # 削除する数字位置インデックスをインクリメント
if rmixix == rmix_list.size(): #
# 問題作成完了
まずは、盤面位置インデックス(0~80)を配列に格納し、シャフルする。
そして配列の最初から順に、その位置の数字を消しても適切な問題(ユニーク解を持つ)かどうかをチェックする。
適切な問題でなかった(解が無い or 解が複数ある)場合は、消した数字を戻す。
筆者が以前作成したアプリは C++ で記述していたために、上記処理は1フレーム(約1/60秒)で余裕で終了したが、 スクリプト言語である GDScript ではそうはいかなかったので、1フレームで一つの数字を消すようにしている。
上記を全配列要素分繰り返すと、初級解法テクニックだけでロジカルに解ける問題が出来上がる。
生成した問題例を下図に示す。
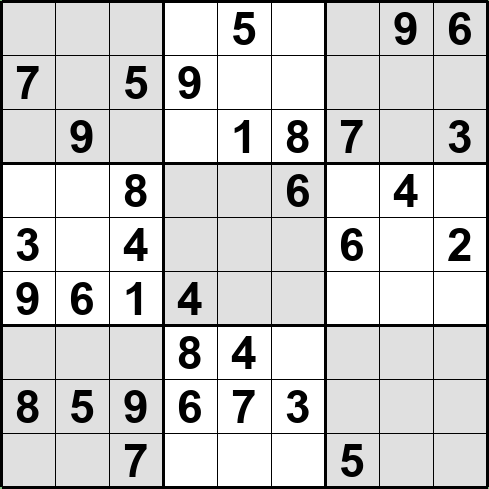
対称形問題生成
株式会社ニコリがナンプレを日本で紹介した時に「数独」という名前を付けた (最初は「数字は独身に限る」という名前であったが、後で「数独」に短縮された)。
さらにその時、問題の手がかり数字を対称形に配置することで、見た目を良くし、 解いてみたいという気持ちを高めるという工夫をした。それが数独成功の一因とも言われている。
というわけで、「さくさくナンプレ」でも、対角線対称の問題を生成可能なようにしている。
対称形問題を生成するには、対称形の元部分の位置インデックスだけの配列を作り、 数字を消すときにその位置だけを消すのではなく、対称位置も同時に消していくとよい。
対称形問題生成コードは以下の通りだ。
func gen_quest_greedy():
gen_ans() # 解答生成
# 対称形の元になる位置のみ rmix_list に追加
for y in range(5):
for x in range(y, N_HORZ - y):
rmix_list.push_back(xyToIX(x, y))
rmix_list.shuffle() # 順番をランダムにするためにシャフル
rmixix = 0 # 次に削除する位置
func _process(delta):
.....
if !rmix_list.empty(): # 問題自動生成中
.....
lst.push_back(xyToIX(x, y)) # 削除位置をリストに追加
lst.push_back(xyToIX(y, x)) # 対称位置もリストに追加
lst.push_back(xyToIX(N_HORZ - 1 - x, N_VERT - 1 - y))
lst.push_back(xyToIX(N_VERT - 1 - y, N_HORZ - 1 - x))
.....
生成した対角線対称形問題例を下図に示す。
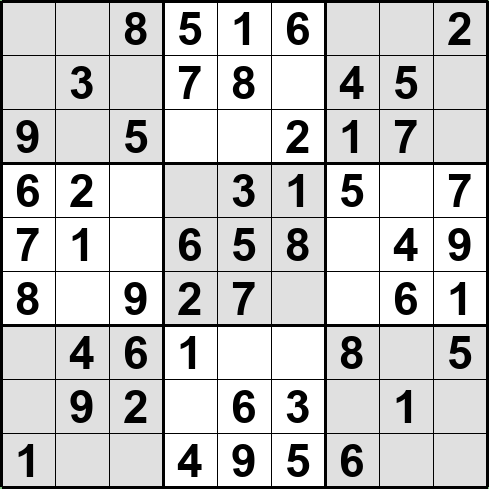
演習問題:上下左右対称問題を生成するよう修正してみなさい
おわりに
拙作「さくさくナンプレ」の問題自動生成プログラムについて解説した。 ビット演算を多用しているので、理解が難しかったところもあったかもしれないが、 なんとなく理解し、全体の流れを把握していただければ幸いだ。
プログラミング言語は Godot の GDScript だったが、これを C++ や C# などに移植してみると理解が深まるかもしれない。 興味ある読者は是非やってみてほしい。
TechProjin Godot入門 関連連載リンク
Godotで学ぶゲーム制作
さくさく理解するGodot入門 連載目次
標準C++ライブラリの活用でコーディング力UP!
「競技プログラミング風」標準C++ライブラリ 連載目次




