今回は【基礎理論編】論理回路演算2 ～ビット演算～について紹介します。
前回の記事で論理演算について学びました。
今回の記事では、その論理演算を利用して、あるビット列から特定のビットを取り出したり、あるビット列の特定のビットを反転させたりする『ビット演算』について説明していきます。
言葉での説明よりも具体例の方が理解しやすいかと思いますので、とりあえず先に進みましょう。
ビット列の取り出し
まずビット列の取り出しから説明していきます。
この処理をもう少し細かく説明すると、『あるビット列と特定のビット列との間でビット演算を行うことで、あるビット列の特定のビットだけを取り出す』ということです。
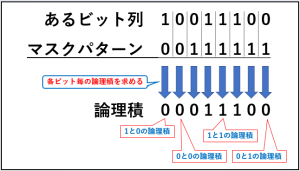
それでもわかりづらいので、2進数8ビット[10011100]を具体例にして説明していきます。
この[10011100]が『あるビット列』にあたります。
ではこのビット列の下位6ビットを取り出したいとしましょう。
つまり[011100]が取り出せればいいというわけです。
ビット列[10011100]と『特定のビット列』との間でビット演算を行うのですが、ここでいう『特定のビット列』とは『操作したいビットに1、操作しないビットに0を入れたビット列』です。
今回の例でいうと、取り出したい下位6ビットが操作対象ということになります。
つまり『特定のビット列』は、今回の場合[00111111]です。
この『特定のビット列』のことをマスクパターン（またはマスク）と呼びます。
というわけで[10011100]の下位6ビットを取り出すために、[10011100]と[00111111]でビット演算を行います。
ビット演算はざっくり説明すると、ビットで論理演算を行うことです。
今回のように『特定のビットだけを取り出す』場合は、論理積を使います。
論理積についてまだ理解できていない方は、前回の記事を読んでから先に進みましょう。
では[10011100]と[00111111]の論理積について考えます。
まとめて8ビットで考えるのではなく、1ビットずつの論理積を求めていきます。
論理積[00011100]が求められました。
この論理積の下位6ビットに注目すると、元のビット列（10011100）の下位6ビットと一致していることがわかります。
そして操作対象でない上位2ビットは0になっています。
これがビット列の取り出しです。
「だから何？」と思うかもしれませんが、このビット演算はIPアドレスとサブネットマスクの処理などに用いられます。
既にサブネットマスクについてご存じの方は「なるほど」と思えるんじゃないでしょうか。
むしろ思えないとダメです。
IPアドレスとサブネットマスクについての記事も今後掲載予定ですので、「サブネットマスクって何？」という方もそちらを読んでいただければ大丈夫です！
ビットの反転
続いてビットの反転について説明します。
こちらは『あるビット列と特定のビット列との間でビット演算を行うことで、あるビット列の特定のビットだけ反転させる』処理になります。
こちらも具体例を使って説明していきます。
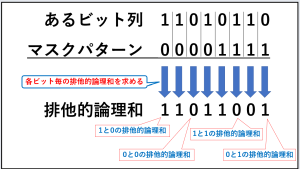
2進数8ビット[11010110]の下位4ビットを反転していきたいと思います。
ビット反転の場合は排他的論理和を使います。
あるビット列とマスクパターンとの排他的論理和を求めるだけです。
排他的論理和について理解が怪しい方は、前回の記事を確認しておきましょう。
今回は下位4ビットが操作対象ですので、マスクパターンは[00001111]となります。
排他的論理和[11011001]が求められました。
この排他的論理和の下位4ビットに注目すると、元のビット列（11010110）と上位4ビットは同じで、下位4ビットだけが反転していることがわかります。
これがビット列の反転です。
ビットの反転はパリティ符号や暗号化の処理などに用いられていますが、この基本情報技術者試験ブログでは扱いませんので、気になる方は調べてみてください。
まとめ
- マスクパターンとは操作対象のビットを1、その他のビットを0にしたビット列
- ビット列の取り出しは、元のビット列とマスクパターンとの論理積をとればよい
- ビット列の反転は、元のビット列とマスクパターンとの排他的論理和をとればよい
演習問題
1.16ビットの2進数の下位4ビットをビット演算で取り出したい場合、マスクパターンを10進数で表記したものとして正しいのは次のうちどれですか？
A.4
B.8
C.15
D.16
2.次のうち、16ビットの値の全ビットを反転させる操作はどれですか？
A.16進数表記00のビット列との論理積をとる
B.16進数表記FFのビット列との排他的論理和をとる
C.16進数表記FFFFのビット列との論理積をとる
D.16進数表記FFFFのビット列との排他的論理和をとる
演習問題の解答は次回の記事で
前回の演習問題の解答
1.
上図の論理回路と等しい回路は次のうちどれですか？
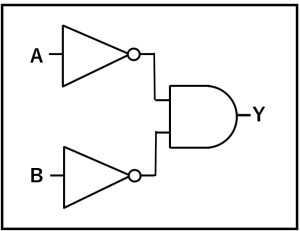
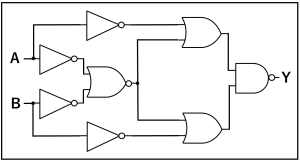
解答：C
解説：YはAの否定とBの否定の論理積、すなわちA・Bということになります。
これをド・モルガンの法則で変形するとA＋B、すなわちAとBの否定論理和ということになるので、正解はCです。
2.
上図の論理回路と等しい回路は次のうちどれですか？
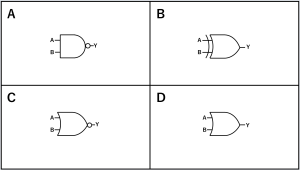
解答：B
解説：一見複雑ですが、1つ1つ処理していけばそこまで難しいものではありません。ベン図、真理値表、ド・モルガンの法則、どれでも求められますが、今回はド・モルガンの法則とベン図を使った解法で進めていきます。
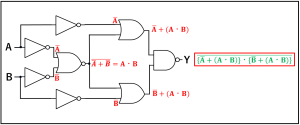
上図のように1つ1つ紐解いていくと、Yを演算記号で表現することができます。
あとはド・モルガンの法則を使って変形していくだけです。
変形ししてできたA・B＋A・Bをベン図を使って表すと
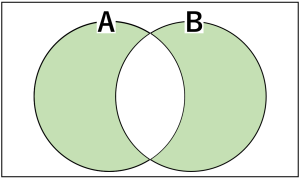
となります。これはAとBの排他的論理和そのものです。よって正解はBです。
