今回は【基礎理論編】論理回路演算1 ~MIL記号~について紹介します。
前回の記事で集合とベン図について学びました。
その記事内にも書きましたが、今回の記事で説明する論理演算はベン図で考えると理解しやすくなります。
まだ前回の内容がよくわかっていない方はもう一度前回の記事を読み直し、しっかり理解してからこの記事を読みましょう。
ざっくり言うと論理演算とは『真の値』と『偽の値』の2つの値を用いて行う演算のことです。
この説明だけだとよくわからないと思いますが、まだわからなくても大丈夫です。
記事を読んでいれば「これが論理演算か」とわかると思うので、ひとまず読み進めちゃってください。
論理和(OR)
論理演算は大きく分けて3種類あります。
まず最初に紹介するのは論理和です。
学生時代に集合の学習で習った方もいるんじゃないでしょうか?
もし論理和という言葉を聞いたことなくても問題ありません。
和集合のことだと思ってもらって差し支えないかと思います。
学生時代の数学の授業を思い出せればこの単元は楽になります。
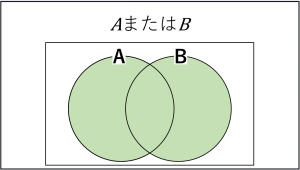
『AとBの和集合』と言われたら『AまたはB』のことでしたね?
記号で表すと『A⋃B』でした。
ベン図を使うと
ですね。
論理和もこれと同じようなものだと思ってください。
ただし論理和では『⋃』ではなく、『+』を使います。
最初に説明したように論理演算は『真の値』と『偽の値』の2つの値を用いて行う演算のことです。
そしてコンピュータ内部では電気信号のON/OFFを1と0に対応させて処理しています。
つまり1を真の値、0を偽の値として論理演算を行います。
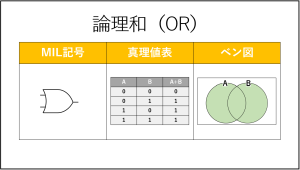
論理和は、入力(A,B)のどちらか一方でも1(真の値)ならば、出力(A+B)が1(真の値)となる演算です。
これだけのことです。
上図中央の真理値表がわかりやすいかと思います。
真理値表は入力に応じた出力結果をまとめた表のことです。
『入力(A,B)のどちらか一方でも1ならば、出力(A+B)が1』なので、入力がどちらも0の時のみ出力が0になっていますね。
複雑な論理演算の問題を解くときはこの真理値表か、前回の記事で紹介したベン図、ド・モルガンの法則のいずれかを使いましょう。
また、論理演算を実際に行う電子回路のことを論理回路といい、CPUに組み込まれています。
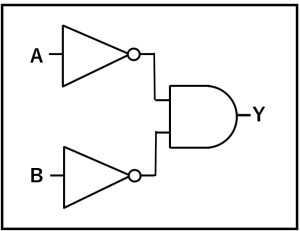
上図左のMIL記号は論理回路を図式化したものです。
MIL記号で論理回路を表現した問題がよく出題されますので、それぞれの論理演算のMIL記号は必ず覚えてください。
文章による説明だけだと論理回路のイメージがわかない方もいると思いますが、記事の最後にある演習問題を見ていただければ大丈夫だと思います。
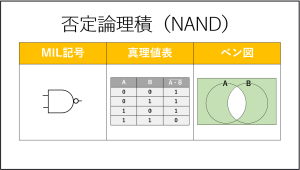
論理積(AND)
続いて論理積について説明します。
なんとなく想像がついていると思いますが、積集合です。
積集合は『AかつB』、記号で表すと『A⋂B』でしたね。
『AとBの共通部分』という言い方をすることもあります。
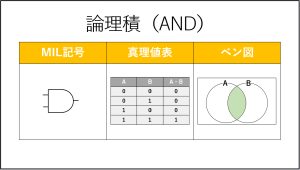
論理積では『⋂』ではなく、『・』を使います。
論理積は、入力(A,B)の両方ともが1であれば、出力(A・B)が1となる演算です。
こちらのMIL記号も必ず覚えましょう。
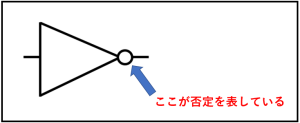
否定(NOT)
3つ目の論理演算は否定です。
何も捻りはありません。そのままです。
いわゆる補集合ですね。
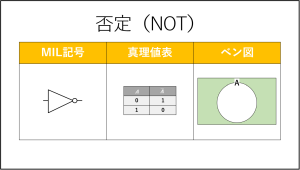
そして否定と補集合は記号も同じ『A』です。
否定は、入力(A)が1であれば出力(A)が0、入力(A)が0であれば出力(A)が1となる演算です。
MIL記号ですが、否定を意味するのは▷の部分ではなく、小さい〇の部分です。
すなわち論理和の否定(A+B)は
となり、論理積の否定(A・B)は
となります。
このように論理和、論理積、否定を組み合わせた演算が論理演算です。
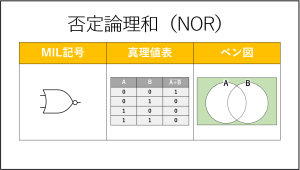
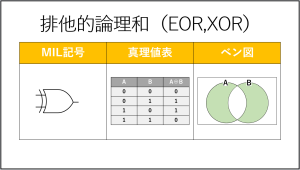
排他的論理和(XORまたはEOR)
最後に排他的論理和について説明します。
まさかの4種類目ですが、『論理演算は大きく分けて3種類』ということは揺るぎません。
排他的論理和も論理和、論理積、否定を組み合わせることで表現ができます。
しかし、排他的論理和には専用の記号が用意されているため、4種類目として紹介します。
排他的論理和は、入力(A,B)が異なれば、出力(A⊕B)が1となる演算です。
本来は論理和、論理積、否定を組み合わせてできる演算にも関わらず、演算記号(⊕)もMIL記号も専用のものがあります。
とはいえ「入力が異なれば1」というシンプルなものですので、覚えてしまえばどうってことはないです。
これでなんとなく論理演算については理解できたと思います。
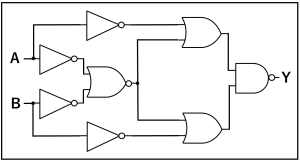
しかしまだMIL記号についてはピンときていない方も多いかと思いますので、演習問題にもしっかり取り組みましょう。
まとめ
- 論理演算は『真の値』と『偽の値』の2つの値を用いて行う演算のこと
- 真理値表は入力に応じた出力結果をまとめた表のこと
- MIL記号は論理回路を図式化したもの
演習問題
演習問題の解答は次回の記事で
前回の演習問題の解答
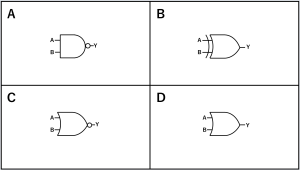
1.Aを偶数全体の集合、Bを素数全体の集合としたとき、『AかつB』として正しい選択肢は次のうちどれですか?
A.{0}
B.{1}
C.{2}
D.{0,2}
解答:C
解説:偶数かつ素数である数は2しかありません。よって正解はCです。
2.任意の集合A,Bにおいて、
![]() と必ず等しくなる選択肢は次のうちどれですか?
と必ず等しくなる選択肢は次のうちどれですか?
A.AかつB
B.AまたはB
C.AかつB
D.AまたはB
解答:C
解説:ド・モルガンの法則を使って1つずつ処理していきましょう。内部から処理するか、一番外から処理するかは自由です。
下図は外から処理する場合の解説になります。
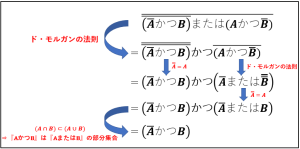
よって正解はCです。