今回は【基礎理論編】集合とベン図について紹介します。
『集合とベン図』について「全く学んだことがない」という方は少ないはずです。
ここでの集合は数学の授業で習った集合のことだと思ってください。
そしてベン図は集合の問題を解くうえで便利なものとして習うことが多いです。
多くの方は既に集合やベン図についてしっかり理解できているのではないかと思います。
そういった方たちにとっては今回の記事は退屈なものになるかもしれません。
少しでも怪しい方は必ずしっかり読んで理解してから先に進んでください。
今回の記事は次回紹介する超重要単元【論理演算】の下準備です。
集合
今更あえて集合という言葉を説明する必要はないかもしれませんが、念のため確認しておきましょう。
集合とは簡単にいうと「モノの集まり」です。
『基本情報技術者の資格を持っている人』『2桁の奇数』『二足歩行の動物』…など、集合の例は無限に存在します。
ただし正確な定義は「集まりに属するかどうか明確に判定できること」ですので、『太っているのに小食な人』のような具体的に線引きがされていないものは数学的に集合とは言えません。
また、集合に属するものを要素(または元)と呼びます。
その他にも色々な用語や記号を習ったと思いますが、それらを覚えなおす必要はないのでご安心ください。
数学で習った集合をそのまま使うわけではありません。
論理演算をやる上でベン図が役に立つのですが、そのベン図を説明するために集合について説明しているだけです。
ベン図
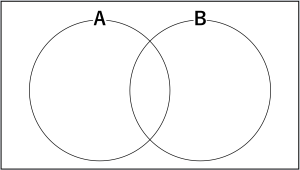
ではベン図の説明に移ります。
「そんなの習ったっけ?」と思った方も、実際に図を見れば「これのことか」となると思います。
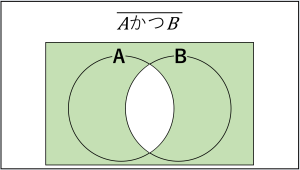
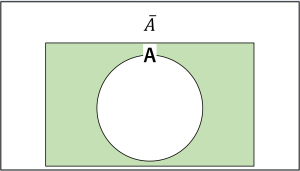
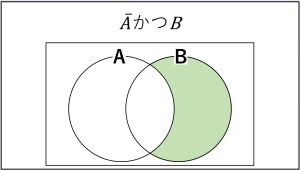
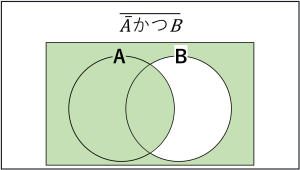
これのことです。
複数の集合の関係を視覚的に表現したものです。
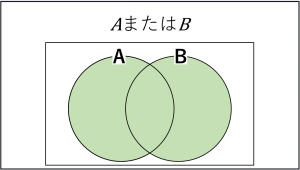
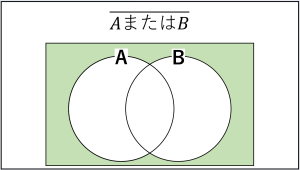
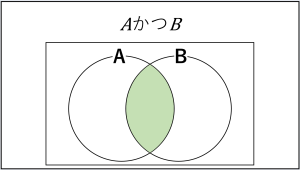
『AかつB』とか『AまたはB』くらいのレベルだったら大したことありませんが、『AかつB』や『AまたはB』(AはAの否定)になってくると、ベン図がないとわかりづらく感じる方が結構出てきます。
さらに複雑なものだと否定が2つ以上重なることもあります。
そうなると数学が得意な人でもベン図無しでは厳しかったりします。
ベン図を使えばそんな複雑な集合の関係性もイメージしやすくなります。
複雑な否定を含むものでも、ベン図さえ書けてしまえばとても簡単ですね。
これを使うと次回説明する論理演算が楽になるので頭に入れておいてください。
ド・モルガンの法則
集合といえばド・モルガンの法則ですよね。
ド・モルガンの法則を知っていればベン図を書く必要がないので、大幅な時間短縮になります。
数学では「または」や「かつ」という言葉ではなく『⋃』や『⋂』という記号を使うのが一般的なので気持ち悪く感じる方もいると思いますが、序盤で「用語や記号は覚えなおさなくてもいい」と言ってしまったので記号は使わずに表現させてもらいました。(下のまとめでは記号を使っています)
何度も否定が重なるような複雑なものも、この法則に従って1つ1つ処理していけば難しくありません。
記事の最後にある演習問題でド・モルガンの法則を実際に利用してみましょう!
まとめ
- 集合とは「モノの集まり」のこと
- 集合の関係性をイメージしやすいように視覚的に表したものをベン図という
- ド・モルガンの法則は(A⋂B=A⋃B, A⋃B=A⋂B)
演習問題
1.Aを偶数全体の集合、Bを素数全体の集合としたとき、『AかつB』として正しい選択肢は次のうちどれですか?
A.{0}
B.{1}
C.{2}
D.{0,2}
2.任意の集合A,Bにおいて、
![]() と必ず等しくなる選択肢は次のうちどれですか?
と必ず等しくなる選択肢は次のうちどれですか?
A.AかつB
B.AまたはB
C.AかつB
D.AまたはB
演習問題の解答は次回の記事で
前回の演習問題の解答
1.次の選択肢のうち、『情報落ち誤差』の説明はどれですか?
A.浮動小数点の加減算において、一方の数値の下位の桁が計算結果に反映されないこと。
B.四捨五入、切り捨て、切り上げなどによって発生する誤差のこと。
C.浮動小数点において演算結果が0に近づき過ぎることで数値が表現できなくなってしまうこと。
D.近い値の浮動小数点同士の引き算において、有効数字が減ってしまうこと。
解答:A
解説:Aが情報落ち誤差の説明です。Bは丸め誤差、Cはアンダーフロー、Dは桁落ち誤差の説明です。
2.次の選択肢のうち、2の補数表現を用いた8ビットの2進数で表すと『桁あふれ』が発生してしまう計算どれですか?
A.14×9
B.(-16)×8
C.8×16
D.(-14)×9
解答:C
解説:A,B,C,Dを10進数のまま計算するとA=126,B=-128,C=128,D-126となります。2の補数表現を用いた8ビットの2進数で表現できる数値の範囲は-128~127なので128は表すことができません。よってCが正解です。