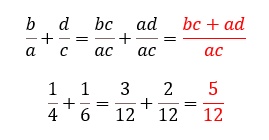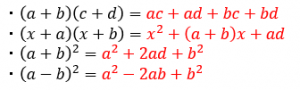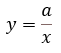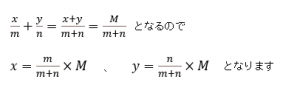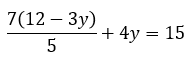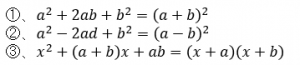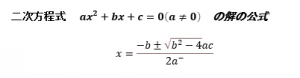各種計算を行う必要がある為最低限の数学知識は必要になりますここでは基礎的な数学知識を
上げていきたいと思います。
【基本】
1、実数の四則計算
足し算、引き算、掛け算、割り算の4つが合わせて四則といいます。
次の3つの法則が計算の基本となります。
・交換法則 a+b=b+a 、ab=ba
・結合法則 (a+b)+c=a+(b+c) 、(ab)c=a(bc)
・分配法則 a(b+c)=ab+ac 、(a+b)c=ac+bc
上記の通り法則に則り式を変形させても同等の結果となります。
2、代数和
(+a)+(-b)+(+c)の事を、a-b+c と書いても良く
(+1)+(-2)+(+3)の事を、1-2+3と書いても良いという事です
これは足し算の+を省略したものでこのような書き方を代数和と言います。
3、分数の四則計算
・約分
分母と分子に共通の文字式や公約数があるときはそれらで分母、分子を
割る事が出来この事を約分と言います。
・通分
2つ以上の分数式で分母が異なる時、それぞれの分数式の分母が同じ整式になるよう
変形することを通分と言います。通分する際には分母がそれぞれの分数式の分母の
最小公倍数になるように分子と分母に同じ整数を掛けます。
4、式の展開
カッコ()を外す事を展開すると言います
式の展開の公式
5、比例式
・比と反批
ある数aが他の数bの何倍かを表す関係を、aのbに対する比またはaとbの比といい、
これをa:b、または
と書きます。
また、a:bの比に対して、その逆のb:aの事を反比または逆比と言います。
・比例式
aとbの比が、cとdの比に等しい式を“比例式”といい、これをa:b=c:d
または
と書きます。
・比例式の性質
比例式でa:b=c:dであるとき
が成立し次の関係となります
┏━内項━┓
a:b = c:d
┗━━━外項━━━┛
①内項の積は外項の積に等しい
②両辺をそれぞれ加えても等しい
・比例と反比例
伴って変わる2つの変数x、yの関係が、y=axと言う式であらわされるとき、
「yはxに比例する」と言います。Xが2倍になるとyも2倍に、xが10倍になると
yも10倍になります。
また、伴って変わる2つの変数x、yの関係が、
と言う式に表されるとき「yはxに反比例する」と言います。
比例、反比例いずれの場合でもaは0でない定数でこのaを比例定数と言います。
・比例配分
いま、ある量をMとして、これを2つの量x、yに分ける時、各比が、m:nとなる
ように分けることを比例配分と言います。
一次方程式の計算
連立方程式の解き方
連立方程式の解き方には、加減法、代入法などがあります
例:次の方程式を解く
┏ 5x+3y=12
┗ 7x+4y=15
代入法を用いた解き方
┏ 5x+3y=12・・・①
┗ 7x+4y=15・・・②
式①より
式③を式②へ代入すると
式④の両辺に5をかけて
7(12-3y)+20y=75
84-21y+20y=75
-y=-9 y=9
式⑤を式③に代入すると
∴x=-3
したがって、x=-3、y=‐3 となります。
二次方程式の計算
二次方程式
(a≠0、a、b、cは実数)を満たすxの値をこの方程式の解または根といいます。
1,因数分解の公式
因数分解とは、単項式の和の形を多項式の積の形に戻す操作をする事を言います。以下に基本的な因数分解の公式をまとめました。
・因数分解の公式
例:次の二次方程式を因数分解してその解を求める
∴ x-3=0 、x-2=0 より x=3 、x=2
2、解の公式
二次方程式は簡単に因数分解出来るとは限りません。そこで一般の二次方程式の解を導き出しておきましょう。
その他の数学知識も必要ですがこれ以外は必要な際に取り上げて行きます。
つづく