const char* 型の比較元文字列 src と、比較先文字列 dst が与えられたとき、その差分を計算したい。
差分計算にあたっては、下図のような格子状のエディットグラフを考える。
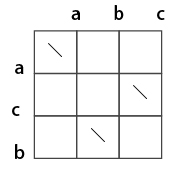
エディットグラフにの上辺に比較元文字列、左辺に比較先文字列の各文字を(囲碁のように交点位置に)配置し、 比較元・先の文字が一致する箇所には「\」を配置する。
そして、最左上点から最右下点への最小コスト経路を考える。ただし、各格子点から右または下に移動する場合のコストは1、 各格子点から「\」を通って右下に移動する場合のコストは0とする。
最小コストを与える経路長を「最小編集距離(Shortest Edit Edistance)」と呼ぶ。なぜなら、右の格子点への移動は1文字削除を、 下の格子点への移動は1文字挿入を表すからだ。
また、最小編集距離を与える経路を「最長共通シーケンス(Longest Common Sequence)」と呼ぶ。
例えば、”abc”, “acb” のエディットグラフの各格子点の最小編集距離は下図のようになり、ゴール地点の最小編集距離は2となる。
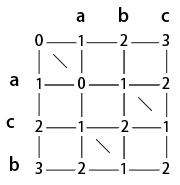
また、上図の最長共通シーケンスは “=a-b=c+b” または “=a+c=b-c” となる。 ただし、「=文字」は文字が等しくエディットグラフ上で右下に進むことを、 「-文字」はsrcの文字を削除すること、すなわちエディットグラフ上では右に進むことを、 「+文字」はdstの文字を挿入すること、すなわちエディットグラフ上では下に進むことを表すものとする。
上記を理解した上で、テストコードの ToDo 部分にコードを記述し、下記のメンバ関数を実装しなさい。
・cchr* 型の引数2つを受け取り、その最小編集距離を返す関数 int SED(cchar* src, cchar* dst)
・cchr* 型の引数2つを受け取り、その最長共通シーケンスを返す関数 string LCS(cchar* src, cchar* dst)
なお、使用するアルゴリズムは、エディットグラフの全格子点の最小編集距離を計算する、単純なものでよいものとする。
[java]
#include <iostream> // 標準入出力ライブラリ
#include <string>
#include <vector>
using namespace std; // std 名前空間使用
typedef const char cchar;
#define DO_TEST(exp) do_test(exp, __LINE__)
void do_test(bool b, int line) {
if( b ) return; // OK
cout << "\nNG at line " << line << "\n";
exit(1);
}
class Diff {
public:
int SED(cchar* src, cchar* dst) { // src, dst の最小編集距離を返す
// ToDo: ここにコードを追加し、src, dst の最小編集距離を返す
return 0;
}
string LCS(cchar* src, cchar* dst) { // src, dst の最長共通シーケンスを返す
// ToDo: ここにコードを追加し、src, dst の最長共通シーケンスを返す
return "";
}
private:
int m_M; // src 文字列長
int m_M1; // m_M + 1
int m_N; // dst 文字列長
int m_N1; // m_N + 1
vector<int> m_v; // 各格子点の最小編集距離1次元配列
};
int main() {
Diff d;
DO_TEST( d.SED("", "") == 0 );
DO_TEST( d.SED("abc", "abc") == 0 );
DO_TEST( d.SED("abc", "ac") == 1 ); // 削除1
DO_TEST( d.SED("abc", "abXc") == 1 ); // 挿入1
DO_TEST( d.SED("abc", "acb") == 2 ); // 削除1, 挿入1
DO_TEST( d.SED("abc", "XYZZZ") == 8 ); // 削除3、挿入5
DO_TEST( d.SED("abcd", "ad") == 2 ); // 削除2
//
DO_TEST( d.LCS("", "") == "" );
DO_TEST( d.LCS("abc", "abc") == "=a=b=c" );
DO_TEST( d.LCS("abc", "ac") == "=a-b=c" ); // 1文字削除
DO_TEST( d.LCS("abc", "abXc") == "=a=b+X=c" ); // 1文字挿入
//
cout << "\nGood Job!\n";
return 0;
}
[/java]
ヒント
・エディットグラフの各格子点の最小編集距離を原点から順に計算していく。
・格子点位置の比較元・先の文字が等しければ、最小編集距離はその左上格子の最小編集距離と同じになる。
・格子点位置の比較元・先の文字が等しくない場合は、その上と左の小さい方+1という値になるぞ。
・最長共通シーケンスを求めるには、エディットグラフをゴールの方から、最小編集距離を与える格子を順に探していくといいぞ。
・格子点位置の比較元・先の文字が等しければ、「=文字」を出力する。
・格子点位置の比較元・先の文字が等しくない場合、その上と左を比べ、上が小さければ「+文字」を、左が小さければ「-文字」を出力するんだぞ。
解答例
[java]
// O(M*N) アルゴリズムを使い src, dst の最小編集距離を返す
int SED(cchar* src, cchar* dst) {
m_M = strlen(src); // 比較元文字列長
m_M1 = m_M + 1;
m_N = strlen(dst); // 比較先文字列長
m_N1 = m_N + 1;
m_v.resize(m_M1 * m_N1); // エディットグラフをリサイズ
//for(auto&x: m_v) x = 0;
int ix = 0;
for(int y = 0; y < m_N1; ++y) {
for(int x = 0; x < m_M1; ++x, ++ix) { // エディットグラスを順に探索 if( y == 0 ) m_v[ix] = x; else { if( x == 0 ) m_v[ix] = y; else { if( src[x-1] == dst[y-1] ) // 文字が等しければ編集距離は増えない m_v[ix] = m_v[ix-m_M1-1]; else // 文字が等しくない場合は、編集距離は上・左の小さい方+1となる m_v[ix] = std::min(m_v[ix-1], m_v[ix-m_M1]) + 1; } } } } return m_v.back(); } // src → dst 最長共通シーケンス(Longest Common Sequence)を求める // return: 最長共通シーケンスを示す文字列を返す // ‘=’: 等しい、 ‘-‘: 削除、’+’: 挿入 string LCS(cchar* src, cchar* dst) { const int slen = strlen(src); SED(src, dst); // 最小編集距離計算 // string lcs; int x = m_M – 1, y = m_N – 1; // エディットグラフ右下から順に最短経路を求めていく while( x >= 0 || y >= 0 ) {
if( x < 0 ) { // 左辺に達している場合
lcs += dst[y–];
lcs += ‘+’;
} else if( y < 0 ) { // 上辺に達している場合
lcs += src[x–];
lcs += ‘-‘;
} else if( src[x] == dst[y] ) { // 文字が等しい場合は左上に移動
lcs += src[x–];
lcs += ‘=’;
–y;
} else { // 文字が等しくない場合は、上・左の編集距離が小さい方に移動
if( m_v[x+1+y*m_M1] <= m_v[x+(y+1)*m_M1] ) {
lcs += dst[y–];
lcs += ‘+’;
} else {
lcs += src[x–];
lcs += ‘-‘;
}
}
}
std::reverse(lcs.begin(), lcs.end()); // 順序反転
return lcs;
}
[/java]
解説
エディットグラフを原点(最左上点)から右方向&下方向に順にスキャンして行けば、全格子点の最小編集距離を求めることができる。 最初に、上辺・左辺の編集距離は 0, 1, 2, … と設定する(左上格子の編集距離は0)。 残りは格子点に対応する文字が一致しているかどうかと、その上・左・左上の最小編集距離から、その格子点の最小編集距離を求める。
具体的には、まず格子点に対応する文字が一致しているかどうかをチェックし、一致していれば挿入・削除は必要ないので、 左上の最小編集距離をその地点の最小編集距離とする。
格子点に対応する文字が一致していない場合は、すぐ上と左の最小編集距離の最小値+1をその地点の最小編集距離とする。
これをゴール地点であるエディットグラフ右下まで繰り返せば、全格子点の最小編集距離が求まる。 そしてゴール地点の最小編集距離が比較元文字列・比較先文字列の最小編集距離となる。
最長共通シーケンスを求める場合は、ゴールから逆に最小編集距離の格子をスタートまでたどっていく。
最小編集距離の場合と同じように、格子点に対応する文字が一致しているかどうかをチェックし、一致していれば「=文字」を出力する。 文字は格子点位置の文字だ(この場合、文字が一致しているので、上辺の文字でも左辺の文字でもよい)。 そして、この場合は左上の格子点に移動する。
格子点に対応する文字が一致していない場合は、すぐ上とすぐ左の格子点の最小編集距離を比較し、その小さい方が最長共通シーケンスとなる。 上が小さければ「+文字」を出力する。このときの文字は挿入文字なので、比較先、すなわち左辺の対応する文字を出力する。 この場合はすぐ上の格子点に移動する。 同様に、左が小さければ「-文字」を出力する。文字は比較元で上辺の対応する文字となる。そしてすぐ左の格子点に移動する。
これを原点まで繰り返せば、最長共通シーケンスが求まる。だが、これだとシーケンスを逆順に求めたことになるので、最後に std::reverse() でシーケンス文字列を反転し、それをメンバ関数の値として返す。







