競技プログラミング風 C++問題集【第11回】

チェスのナイトは上下左右4方向に2マス進んで、進行方向左に１マスまたは右に１マス、合計８箇所に進むことができる。 将棋の桂馬は２箇所に進むことができるので、チェスのナイトは「八方桂」とも呼ばれる（下図参照）。

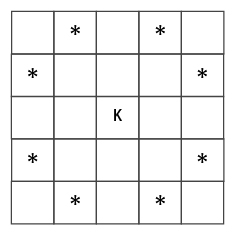
wd x ht の盤面において、ナイトを動かして各マスを全て通り、かつ元に戻ってくる問題を「クローズド・ナイト・ツアー」と呼ぶ。

本問題の盤面データ構造は下図のような1次元配列を使用し（マス内の数字は配列インデックス）、 処理を高速化するために、各マスから移動可能なマスをその下のように予め計算し、m_connects に格納しておくものとする。

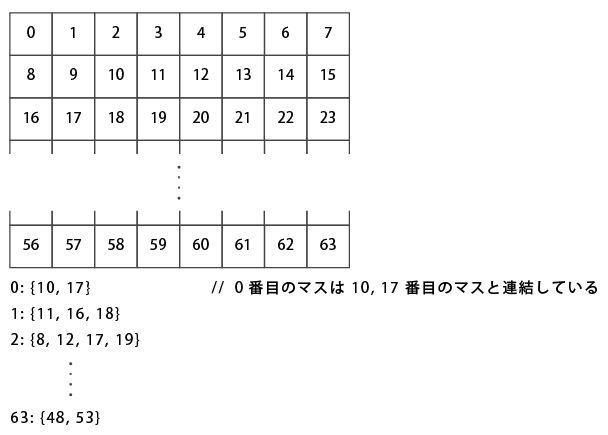
上記を理解した上で、以下のメンバ関数を実装し、クローズド・ナイト・ツアーの解の数を計算可能にしなさい。

・盤面幅・高さを引数で受け取り、クローズド・ナイト・ツアーの解の数を返すメンバ関数 int Board::countKnightTour(int wd, int ht)
・ナイトが ix に来た場合、その移動可能先の連結数を増やすメンバ関数 void incNConnect(int ix)
・ナイトが ix に来た場合、その移動可能先の連結数を減らすメンバ関数 bool decNConnect(int ix, int& ix1)
・ナイトが ix 位置にn番目に移動した場合の処理を行うメンバ関数 void KnightTour(int n, int ix)
[java] #include <iostream> // 標準入出力ライブラリ
#include <vector>
#include <string>
using namespace std; // std 名前空間使用
typedef unsigned char uchar;
#define DO_TEST(exp) do_test(exp, __LINE__)
void do_test(bool b, int line) {
if( b ) return; // OK
cout << "\nNG at line " << line << "\n";
exit(1);
}
class Board {
public:
Board(int wd = 10, int ht = 3) {
setSize(wd, ht);
}
public:
inline int xyToIX(int x, int y) const { return x + y * m_BD_WIDTH; }
inline bool isInner(int x, int y) const { return x >= 0 && x < m_BD_WIDTH && y >= 0 && y < m_BD_HEIGHT; }
void printNth() const { // m_nth[] 盤面表示
for (int y = 0; y < m_BD_HEIGHT; ++y) {
for (int x = 0; x < m_BD_WIDTH; ++x) {
auto t = to_string((int)m_nth[x+y*m_BD_WIDTH]);
if (t.size() < 2) t = ‘ ‘ + t;
cout << t << " ";
}
cout << "\n";
}
cout << "\n";
}
void printConnects() const { // 連結数、連結リスト表示
for (int i = 0; i != m_BD_SIZE; ++i) {
cout << i << ": " << (int)m_nConnect[i] << " {";
for (auto& x : m_connects[i]) cout << (int)x << ", "; cout << "}\n";
}
cout << "\n";
}
void setSize(int wd, int ht) { // サイズ設定
m_BD_WIDTH = wd;
m_BD_HEIGHT = ht;
m_BD_SIZE = wd * ht;
// nth 配列初期化
m_nth.resize(m_BD_SIZE);
for(auto& x: m_nth) x = 0;
// 連結リスト初期化
m_nConnect.resize(m_BD_SIZE);
m_connects.resize(m_BD_SIZE);
int ix = 0;
for (int y = 0; y < ht; ++y) {
for (int x = 0; x < wd; ++x, ++ix) {
m_connects[ix].clear();
if (isInner(x – 1, y – 2)) m_connects[ix].push_back(xyToIX(x – 1, y – 2));
if (isInner(x + 1, y – 2)) m_connects[ix].push_back(xyToIX(x + 1, y – 2));
if (isInner(x – 2, y – 1)) m_connects[ix].push_back(xyToIX(x – 2, y – 1));
if (isInner(x + 2, y – 1)) m_connects[ix].push_back(xyToIX(x + 2, y – 1));
if (isInner(x – 2, y + 1)) m_connects[ix].push_back(xyToIX(x – 2, y + 1));
if (isInner(x + 2, y + 1)) m_connects[ix].push_back(xyToIX(x + 2, y + 1));
if (isInner(x – 1, y + 2)) m_connects[ix].push_back(xyToIX(x – 1, y + 2));
if (isInner(x + 1, y + 2)) m_connects[ix].push_back(xyToIX(x + 1, y + 2));
}
}
// 連結数配列初期化
for (int i = 0; i != m_BD_SIZE; ++i) {
m_nConnect[i] = (uchar)m_connects[i].size();
}
}
// ix に連結しているセルの連結数を減らす
// 連結数が1になったセルがあれば、そこに強制移動になるので ix1 にその位置を設定
// 連結数が1になったセル複数ある場合はデッドエンドなので false を返す
bool decNConnect(int ix, int& ix1) {
// ToDo: ここにコードを追加し、ナイトが ix に来た場合、その移動可能先の連結数を減らす
return true;
}
void incNConnect(int ix) {
// ToDo: ここにコードを追加し、ナイトが ix に来た場合、その移動可能先の連結数を増やす
}
void KnightTour(int n, int ix) {
// ToDo: ここにn番目のナイトが ix 位置に移動した場合の処理を追加
}
int countKnightTour(int wd, int ht) {
return 0; // ToDo: ここにコードを追加し、wd x ht 盤面でのクローズド・ナイト・ツアーの解数を返す
}
private:
int m_count = 0;
int m_BD_WIDTH; // 盤面幅
int m_BD_HEIGHT; // 盤面高
int m_BD_SIZE;
vector<uchar> m_nth; // 何番目にそのセルを訪れたか（1..盤面サイズ）
vector<uchar> m_nConnect; // 各セル連結数
vector<vector<uchar>> m_connects; // 各セルと連結しているセルインデックスリスト
};
int main() {
Board bd;
DO_TEST( bd.countKnightTour(3, 3) == 0 );
DO_TEST( bd.countKnightTour(10, 3) == 16 );
DO_TEST( bd.countKnightTour(3, 10) == 16 );
DO_TEST( bd.countKnightTour(6, 5) == 8 );
DO_TEST( bd.countKnightTour(6, 6) == 9862 );
DO_TEST( bd.countKnightTour(6, 7) == 1067638 );
cout << "\nGood Job!\n";
return 0;
}
[/java]