ソルバー(承前)
今回は乗算・除算ソルバーについて解説する。
乗算ソルバー
乗算問題も加算ソルバーと同じ様に空欄に ‘0’-‘9’ の数字を入れながら深さ優先探索を行えばよい。
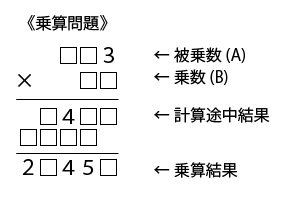
乗算問題の場合は上図の様に空欄の数が多いので、探索時間が膨大になるのではないかと心配されるかもしれない。
しかし、実は全部の空欄について探索する必要は無い。
最初の2行:A*B(被乗数・乗数)の部分がすべて確定すると3行目以降の計算途中結果・乗算結果が決まるので、
それらが問題と一致するかをチェックするとよい。
つまり、A,B の部分の空欄のみを全探索すれば充分ということだ。
たとえば、上図の問題で、最初の2行が 123*45 だとすれば
123*45|615 492|5535 となり、これを問題と比較すると不一致なので、
次の数字を入れて探索を継続することになる。
よって、4桁*4桁問題程度までは単純な深さ優先探索でも短い計算時間で解を得ることができる。
まずは空欄を考慮した一致判定から実装していく。コードは以下のようになる。
加算ソルバーの時に使用した isMatch() は単純に文字列を数値に変換し比較するだけだったが、
isMatchEx() では問題文の文字が ‘*’ の場合は、すべての数値と一致するようにする。
なので、数値を文字列に変換してから、各桁ごとに比較をしている。
bool isMatchEx(const string &t, int v) // 計算結果(t) と v がマッチしているか? t は'*' を含んでいてもよい
{
const auto vs = to_string(v); // 数値を文字列変換
if( vs.size() != t.size() ) return false; // 桁数不一致の場合
for (int i = 0; i != t.size(); ++i) {
if( t[i] != '*' && t[i] != vs[i] ) // '*' はすべての文字とマッチ
return false;
}
return true;
}
次は、A*B 部分の空欄に数値を入れた式が正しいかをチェックする checkMul() を定義する。
計算途中結果・乗算結果の空欄は空欄のままなので、A, B から1桁ごとにそれらを計算し、
isMatchEx() を使って一致するかどうかをチェックする。不一致であれば false を返す。
すべて一致し、引数 fill が true の場合は、計算途中結果・乗算結果を第1引数の vs に格納している。
// A*B が確定した状態でコールされる
bool checkMul(vector<string> &vs , bool fill = false) // fill: 答えを埋めるかどうか
{
int A = atoi(vs[0].c_str()); // Aの値
const auto &bstr = vs[1]; // B文字列
int ln = 2;
for (int i = bstr.size(); --i >= 0; ++ln) { // Bの下の桁から順に掛け算を行う
if( bstr[i] != '*' ) {
int d = bstr[i] - '0';
if( !isMatchEx(vs[ln], d*A) ) // vs[ln] は '*' を含んでいてもよい
return false;
}
}
int B = atoi(bstr.c_str()); // Bの値
if( !isMatchEx(vs[ln], B * A) )
return false;
if( fill ) { // fill 指定されている場合は、計算途中結果・答えを埋める
ln = 2;
for (int i = bstr.size(); --i >= 0; ++ln) {
int d = bstr[i] - '0';
vs[ln] = to_string(d*A);
}
vs[ln] = to_string(B*A);
}
return true;
}
以上で、準備が整ったので、1行・1桁目から順に空欄の数字を決めていき、式が成立しているかをチェックしている。
解はひとつだけ(問題が適切)と仮定しているので、解をひとつ見つけた時点で探索を中止し true を返す。
bool solveMul(vector<string> &vs, int row, int col) // row行、col文字目の次から決めていく
{
for (;;) {
auto ch = vs[row][++col];
if( ch == '*' ) {
for (ch = !col ? '1' : '0'; ch <= '9'; ++ch) {
vs[row][col] = ch;
if( solveMul(vs, row, col) )
return true;
}
vs[row][col] = '*';
return false; // 解未発見
}
if( ch >= '0' && ch <= '9' ) continue;
if( ch == '\0' ) {
if( ++row < 2 ) {
col = -1;
continue;
}
// A * B が確定した場合
return checkMul(vs, true);
}
}
}
bool solveMul(std::vector<std::string>& vs)
{
return solveMul(vs, 0, -1);
}
乗算ソルバーを実際に使用する場合は、下記の様に、問題を文字列配列に設定しsolveMull(vs1)をコールするだけだ。
解が見つかった場合は true を返すので、必要があれば if 文でチェックするとよい。
printMulQuest() の実装については github 参照。
vector<string>vs = {"**3", "**", "*4**", "****", "2*45*"}; // 乗算問題
if( solveMul(vs) ) {
printMulQuest(vs); // 解を表示
} else {
// 解けなかった旨表示
}
除算ソルバー
乗算問題も加算乗算同様に空欄に ‘0’-‘9’ の数字を入れながら深さ優先探索を行えばよい。
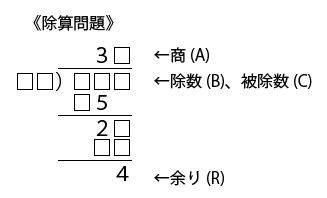
除算問題も上記のように空欄の数が多いが、商・除数・余りを決めれば
除数、計算途中計算結果はユニークに決まる(被除数 = 商*除数 + 余り)ので、
商・除数・余り部分の空欄についてのみ深さ優先探索を行えばよい。
そして計算途中結果・除算結果が問題と一致なら解発見となる。
下記が除算として式が成立しているかをチェックする関数だ。
// 割り算として成立しているかどうかをチェック
// A, B, R(商, 除数, 余り)は確定してるものとする
bool checkDiv(vector<string> &vs , bool fill = false) // fill: 答えを埋める
{
// C / B = A … R(被乗数 / 除数 = 商 … 余り)
const auto &astr = vs[0]; // 商文字列
int A = atoi(astr.c_str()); // 商
int B = atoi(vs[1].c_str()); // 除数
int R = atoi(vs.back().c_str()); // 余り
int C = A * B + R; // 被除数
if( !isMatchEx(vs[2], C) ) // 答えが合っているか?
return false;
int sc = 1;
for (int i = 1; i != astr.size(); ++i) {
sc *= 10;
}
int sc0 = sc;
int ln = 3;
for (int i = 0; i != astr.size(); ++i, ln+=2) {
int d = astr[i] - '0';
if( !isMatchEx(vs[ln], d*B) ) // 除数と商の各桁を掛けたものが一致するか?
return false;
C -= d*B*sc; // 現被除数から除数と商の各桁を掛けたものを引く
if( (sc /= 10) == 0 ) sc = 1;
if( !isMatchEx(vs[ln+1], C/sc) ) // それが一致するか?
return false;
}
if( C != R ) // 余りが不一致の場合
return false;
if( fill ) { // fill 指定されている場合は、計算途中結果・答えを埋める
C = A * B + R; // 被除数
vs[2] = to_string(C);
int ln = 3;
sc = sc0;
for (int i = 0; i != astr.size(); ++i, ln+=2) {
int d = astr[i] - '0';
vs[ln] = to_string(d*B);
C -= d*B*sc;
if( (sc /= 10) == 0 ) sc = 1;
vs[ln+1] = to_string(C/sc);
}
}
return true;
}
以上で、準備が整ったので、1行・1桁目から順に空欄の数字を決めていき、
式が成立しているかをチェックする。
乗算との違いは、商、計算途中はスキップし、余りの空欄数字を決めている点だ。
解はひとつだけと仮定しているので、解をひとつ見つけた時点で探索を中止しtrue を返す。
bool solveDiv(vector<string> &vs, int row, int col, bool fill = true) // row行、col文字目の次から決めていく
{
for (;;) {
if( row == vs.size() ) // A, B, R が確定した場合
return checkDiv(vs, fill);
if (row >= 2 && row < vs.size() - 1) {
row = vs.size() - 1;
continue; // 商、計算途中はスキップ
}
auto ch = vs[row][++col];
if( ch == '*' ) {
for (ch = !col ? '1' : '0'; ch <= '9'; ++ch) {
vs[row][col] = ch;
if( solveDiv(vs, row, col) )
return true;
}
vs[row][col] = '*';
return false; // 解未発見
}
//if( ch >= '0' && ch <= '9' ) continue;
if( ch == '\0' ) {
++row;
col = -1;
}
}
}
bool solveDiv(std::vector<std::string>& vs)
{
return solveDiv(vs, 0, -1);
}
除算ソルバーを実際に使用する場合は、下記の様に、問題を文字列配列に設定しsolveMull(vs1)をコールするだけだ。
解が見つかった場合は true を返すので、必要があれば if 文でチェックするとよい。
printDivQuest() の実装については github 参照。
vector<string>vs = {"3*", "**", "***", "*5", "2*", "**", "4"}; // 除算問題
if( solveDiv(vs) ) {
printDivQuest(vs); // 解を表示
} else {
// 解けなかった旨表示
}
以上でソルバーの解説は終わりだ。以下にソルバーのまとめを記述しておく。
ソルバーのまとめ:
・探索空間が10^6程度であれば、単純な深さ優先探索で解が求まる。
・乗算問題は被乗数・乗数部分のみ、除算問題は商・除数・余り部分のみを探索する
・大部分の一般人向け問題は単純な深さ優先探索で1秒未満で解が求まる。
・より大きな桁数の乗除算問題を解くにはなんらかの枝刈りを行い、
探索空間を狭める必要がある。
課題
「SEND + MORE = MONEY」のようにアルファベットがある問題にも対応したソルバーを作ってみなさい
関連記事
投稿が見つかりません。
 |
筆者:津田伸秀 プロフィール:テニス・オセロ・ボードゲーム・パズル類が趣味の年齢不詳のおじさん。 自宅研究員(主席)。vi と C++が好き。迷走中・・・ ボードゲーム・パズル系アプリ開発・リリースしてます。 |




