今回は【基礎理論(アルゴリズム)編】データ探索についてご説明します。
データ構造やアルゴリズムとも関連する話が出てくるので、わからなければ以前の記事を参考にしながら読んでみてください。
線形探索法/番兵法について
まずは基本的な探索方法について説明していきたいと思います。
線形探索法とは、先頭から末尾までひとつずつ値を確認していくことで探したい値を見つける方法です。
この探索法は極めて単純な探索法なので、探したい値が先頭にあれば1回目で見つけることができますが、もし探したい値が末尾にあるとなると、計算量が大幅に増えてしまいますね…
さて、線形探索法では、探したい値がデータ上に存在しない事も考えておかなければなりません。
(探したい値がどこにもないのにいつまでも探しているわけにはいきません!)
つまり線形探索法は「探したい値が見つかる」または「データを最後までチェックし終わる」まで探索を行うことになります。
どちらかの条件を満たすまで探索処理を続けるので、以前の記事でご紹介した繰り返し処理と条件判定が使えそうですね!
この場合、「探したい値が見つかったかどうか」と「データを最後までチェックしたかどうか」を条件判定として行うことになりますが、繰り返し処理を行うたびにこの2つの条件判定を行うのは少し手間です。
次に説明する番兵法は、この点に関して改良を加えた探索法になります。
番兵法では、データの探索を行う前に探したい値を配列の末尾に追加しておきます。そうすると、単純に「探したい値が見つかる」まで探索を行えばよいことになります。(探したい値が配列上にないことを考慮する必要がなくなりました!)
これによって条件判定の数が2つから1つに減ったので、より効率的に検索を行えるようになるわけです。
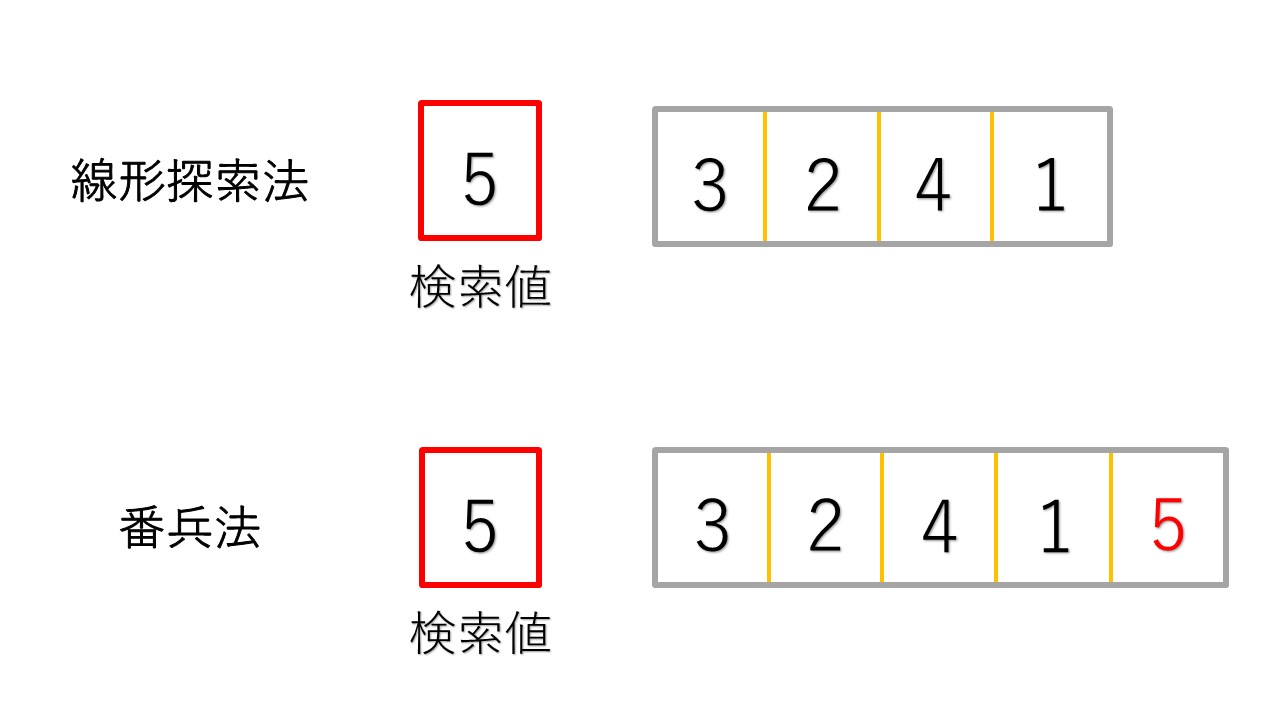
下の図は配列の中からデータを探索するときの線形探索法と番兵法の違いをイラストにしたものです。
番兵法の場合は探したい5という値を配列の末尾に入れてから探索を行います。
二分探索法について
二分探索法は、ソートされたデータに対して有効な探索法の一つです。
例として、前から小さい順に並べられた配列を考えてみましょう。
この探索法では、まず初めに配列中央にあるデータと探したい値とを比較します。
この時、探したい値が配列中央の値より小さければ、配列の前半部分に探したいデータがあると考えられます。
逆に、探したい値が配列中央の値より大きければ、配列の後半部分に探したい値があると考えられますね。
また、配列中央の値と探したい値が等しい場合はその場で探索終了です。
この考え方を使えば、探索対象のデータを一度の比較で半分に減らすことができます!
2度行えばさらにその半分、3度行えばそのまた半分・・・といったように、非常に効率的にデータを絞っていくことができます。
次のイメージ図で確認してみてください。
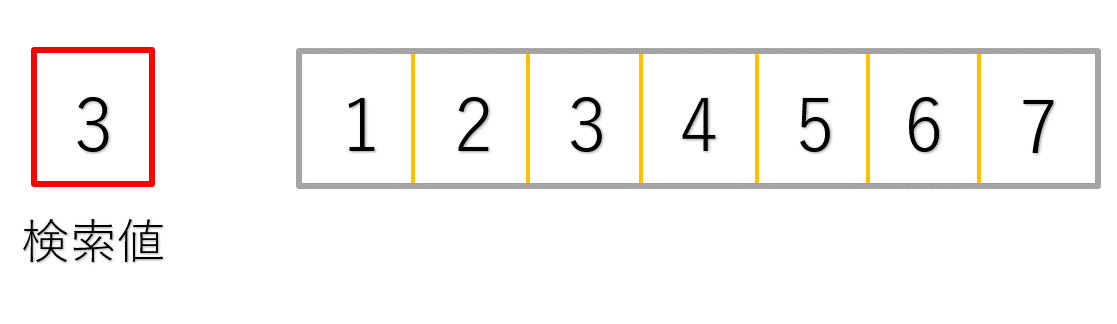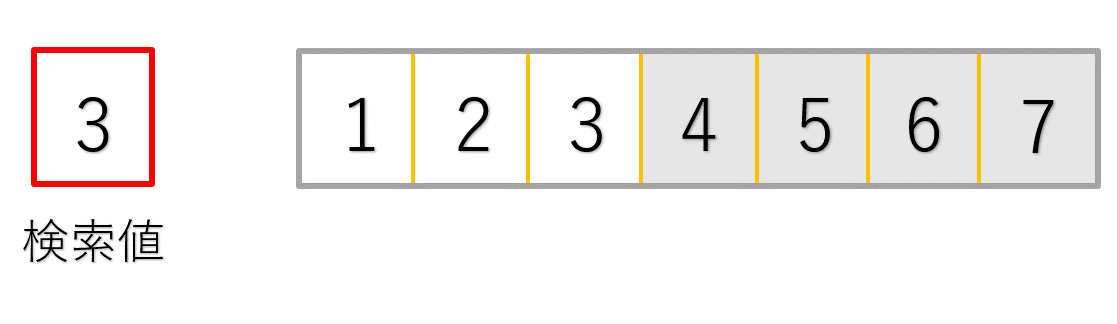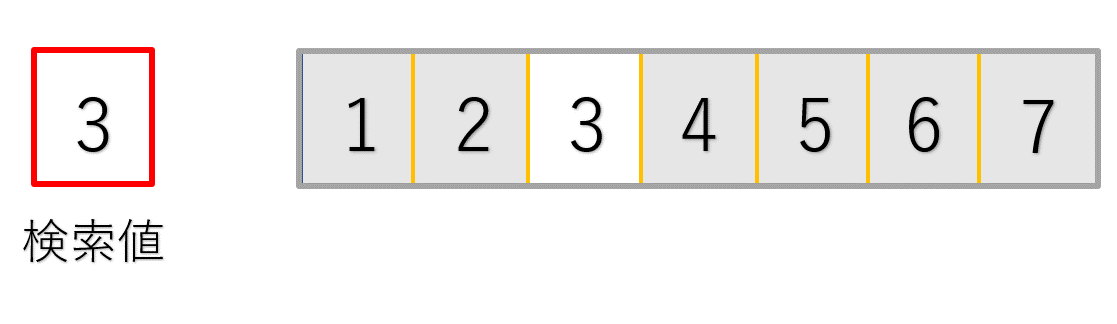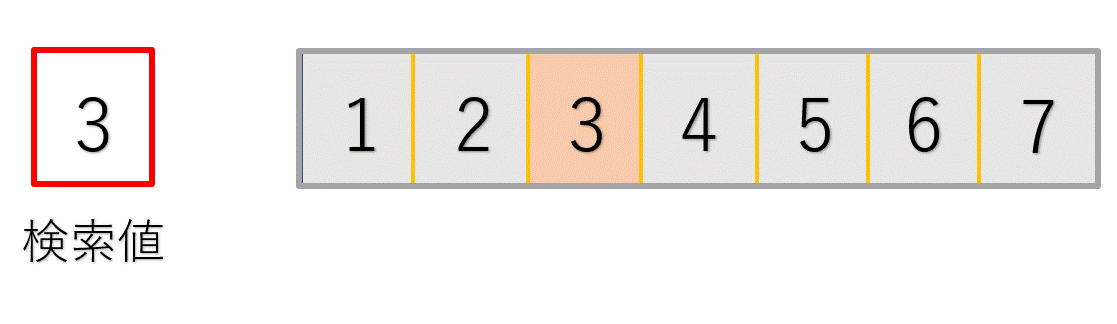
最初の処理では探したい3という値と、配列中央の4という値を比較しています。
3は4よりも小さいので、4以降のデータは確認する必要がないことが分かりますね!(グレーアウトした部分です)
このように、二分探索法はあらかじめデータをソートしておく必要がありますが、そのあとのデータ探索は非常に高速に行えます。
ハッシュ探索法について
ハッシュ探索法は、特定のルールに従ってデータを保管しておくことで探索を高速化しています。
こちらも配列を使った例を挙げて考えてみましょう。
今回は特定のルールとして、「5で割った余りと同じ添え字の位置にデータを格納する」というルールを用いたいと思います。
このルールに従ってデータを格納すると、次のような配列が得られるはずです。

7を5で割った余りは2…といった具合に、各データに対して特定の計算を行うことでデータの格納場所を確定させています。
では、この配列の中から14というデータを探したい場合はどうしたらよいでしょうか?
まずはデータを格納した時と同じように、5で割った余りを考えてみます。
14を5で割った余りは4ですから、配列の添え字が4になっているところを探せば14が格納されているはずです!
格納場所である添え字が分かるので、探索はピンポイントに行えますね!
さて、今回は「格納したいデータを5で割った余り」というルールに基づいてデータの格納場所を決めましたが、このようにデータの格納場所を算出するためのルール(計算式)をハッシュ関数と呼び、ハッシュ関数によって求められた値をハッシュ値と呼びますので覚えておきましょう。
また、勘のいい方はお気づきになっているかもしれませんが、ハッシュ関数によってはハッシュ値、即ちデータの格納場所が被ってしまう可能性があります。
例えば、3というデータを5で割った余りは3ですが、8というデータを5で割った余りも3になります。
ということは、この2つのデータは配列上の同じ場所に格納しなければならないということになります。
このように、格納したいデータが同じハッシュ値をもってしまうことをシノニムの発生と呼びます。
ハッシュ探索法では全てのハッシュ値が等しい確率で生成されるようにハッシュ関数を決めておくことで、ハッシュ値が偏ってシノニムが多く発生することをなるべく避けるようにするのが良いとされています。
この時、ハッシュ値は一様分布と呼ばれる分布になるので、この一様分布が理想状態であることを覚えておきましょう。
これでデータ探索に関する説明は終わりになります。
それぞれのデータ探索法がどのように処理を効率化しているのかをよく押さえておきましょう。
まとめ
- 基本探索法はデータを先頭から順番に探していく方法
- 番兵法は配列の末尾に探したいデータを配置しておくことで探索処理を効率化する
- 二分探索法は配列の中央値と探したいデータとを比較することで探索対象となるデータを半分に絞っていく
- ハッシュ探索法はハッシュ値を用いて格納場所を定め、探索を高速化する
- 理想のハッシュ値の分布は一様分布
演習問題
1.基本探索法/番兵法について誤っている記述を選択してください
A.番兵法と比べて基本探索法の方が効率よく探索ができる。
B.基本探索法と番兵法はどちらも「先頭から順番にデータを探していく」探索方法である。
C.番兵法は配列の末尾に探したいデータを配置しておく
2.二分探索法について最も適切な記述を選択してください。
A.1回の処理で探索範囲が半分になる。
B.探したいデータを配列の先頭から順番にチェックする。
C.ヒープ木を用いて探索を行う。
D.ハッシュ値にしたがってデータの格納場所を算出する。
3.ハッシュ探索法について最も適切な記述を選択してください。
A.算出したハッシュ値が異なっている状態のことをシノニムと呼ぶ
B.理想的なハッシュ値の分布は二項分布である
C.ハッシュ値が多くかぶっている方が効率的に探索ができる
D.理想的なハッシュ値の分布は一様分布である
答えは次回の記事で確認してください。
前回の演習問題~解答例
1.解答:C
解説:
A.シェルソートに関する記述です。
B.ヒープソートに関する記述です。
C.正しい記述です。この基準値のことをピボットと呼びます。
D.基本交換法に関する記述です。
2.解答:B
解説:ヒープ木とは、「全ての要素が親>子(または子<親)という制約に従って配置された二分木」のことです。それを踏まえたうえで選択肢を見ていきましょう。
A.2と3の順番が逆なら全ての要素が親<子の関係をもつヒープ木になります
B.親>子のヒープ木になっています
C.4と9の順番が逆なら親<子の関係をもつヒープ木になります
D.7と9の順番が逆なら親>子の関係をもつヒープ木になります
なお、選択肢Dは一部親=子の関係になっている要素がありますが、ヒープ木においては同値の関係になっていても問題ないので注意しておきましょう。