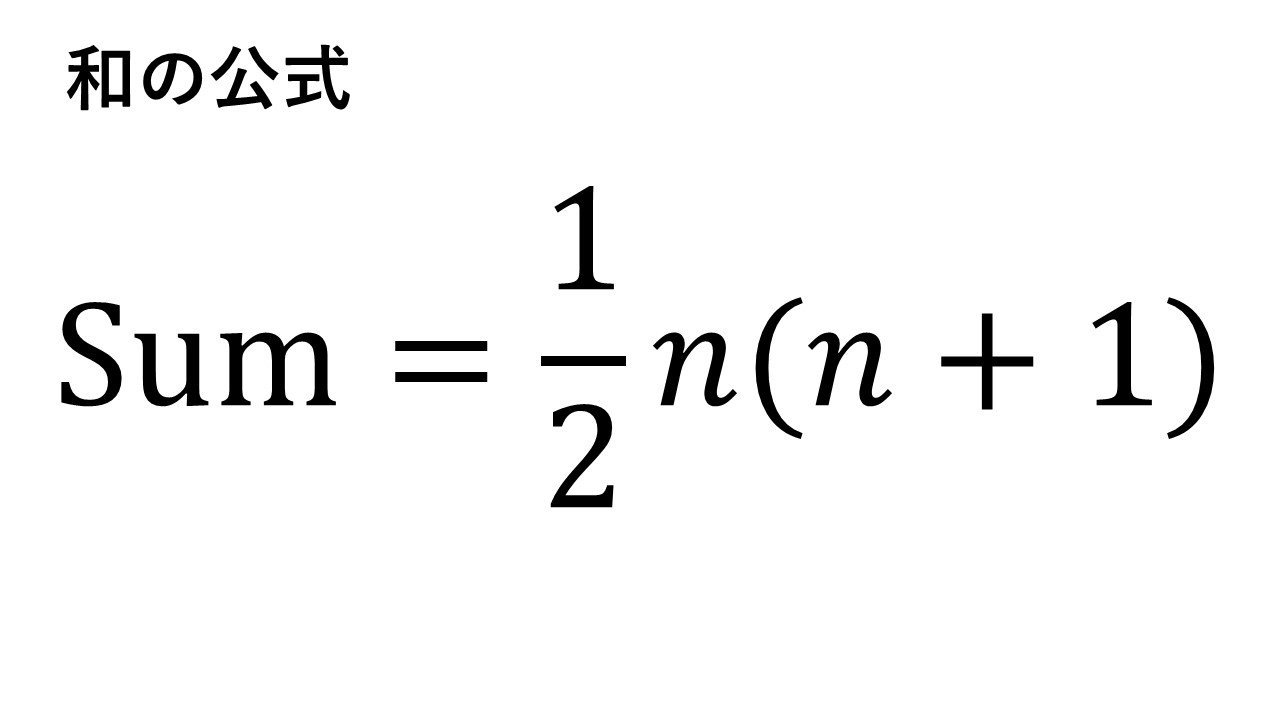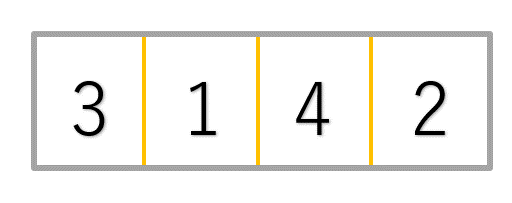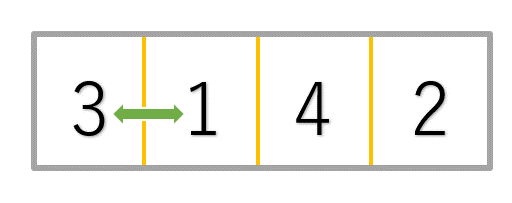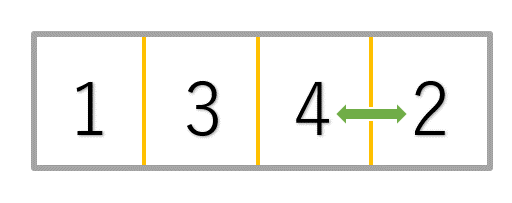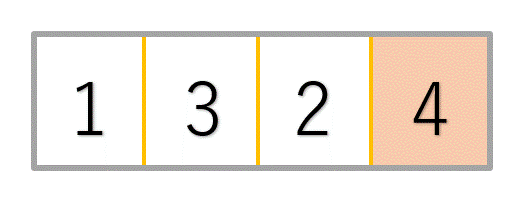今回は【基礎理論(アルゴリズム)編】データ整列 ~基本交換法・選択法・挿入法~についてご紹介します。
試験で出題されるデータ整列法には多くの種類がありますが、今回はその中でも基本的な手法について説明していきたいと思います。
データの整列・比較回数について
データの整列とは、バラバラに並んだデータを、特定の基準にしたがって並べ替えることを指します。
例えば、数値であれば“数字の大小関係”、文字であれば“辞書順”で並び替えることなどが考えられますね!
この時、1,2,3,4・・・のようにデータの小さいものから順に並べていく方法を昇順、
100,99,98,97,・・・のようにデータの大きいものから順に並べていく方法を降順と呼びます。
さて、データを並び替えるためには、何回もデータ同士を比較して順番を組み替えていく必要があります。
この比較回数が少なければ少ないほど高速にデータを整列できることになるので、
本記事では整列方法を学びながら比較回数についても考えていきたいと思います。(試験でも実際に問われています…!)
というわけで、比較回数を算出するための数学的な知識を押さえておきましょう!
突然ですがみなさん、1+2+3+4+・・・+8の計算をしてみてください。
…左から順番に足し上げて計算していますか??
実はこれ、少し工夫をすると綺麗に計算ができます。
1+2+3+4+5+6+7+8 → (1+8)+(2+7)+(3+6)+(4+5) → 9+9+9+9 とすると、どうでしょう…?
1+2+・・・+8の計算は9が4つの計算に等しくなりましたね。つまり(8+1)が8/2個できました。
これを一般化すると1+2+・・・+nの計算をする際には(n+1)がn/2個生まれると考えて、n(n+1)/2で計算ができることが分かります。
これを和の公式として覚えておきましょう!
基本交換法について
さて、ここからは具体的な整列方法について説明していきたいと思います。
基本交換法とは、隣り合うデータ同士を比べて、データの大小関係が逆だった場合には順番を入れ替えていく整列手法のことです。
先頭から末尾にかけてこの操作を行うと、最も大きいデータを末尾に移動させることが出来ます。
分かりづらいのでイラストを確認してみましょう!
隣同士を比較していくことで、4という最大値が末尾に移動したことが分かると思います。
この時点で4番目の値は整列済みと考えることができますよね!
ということは、先頭から3番目までに対して同じ処理を行えば、次は3番目の値を整列済みにすることができそうです。
これを繰り返していくことで全てのデータを整列させることができるのが基本交換法になります。
一度全体の流れを確認してみましょう。(整列済みの値は赤色にしてあります)

これが基本交換法の整列イメージです。
泡が水面に浮かびあがっていくようにデータが移動していくので、別名バブルソート(または隣接交換法)と呼ばれています。
では、基本交換法の比較回数はいくらになるでしょうか?
データの数が全部でn個だとすると、
1巡目の比較回数は、n-1回です。(4つのデータがある上の例では3回の比較で済みましたね!)
2巡目では末尾のデータが整列済みなので、それより一回分少ない比較回数で済み、n-2回の比較になります。
3巡目はn-3回、4巡目はn-4回・・・ときて、最後は1回の比較で終わりますね。
つまり基本交換法の比較回数は(n-1)+(n-2)+(n-3)+・・・+1となります。
先ほど紹介した和の公式を使うと、総比較回数が(n-1)n/2であると計算できますね!
ただし、これは比較的重いソート処理になってしまいます…
基本選択法について
基本選択法とは、全体のデータから最大値となるデータを選択して末尾と入れ替えていく整列手法のことです。
先ほどの基本交換法と同じように、1巡目が終わると末尾のデータが整列済みになるので、
残りのデータに対して同じ操作を繰り返していけば全てのデータを整列させることができそうです。
もちろん、全体のデータから最小値を探し出して、それを先頭と入れ替えていく方法でも整列可能で、その場合も基本選択法と呼ばれます。
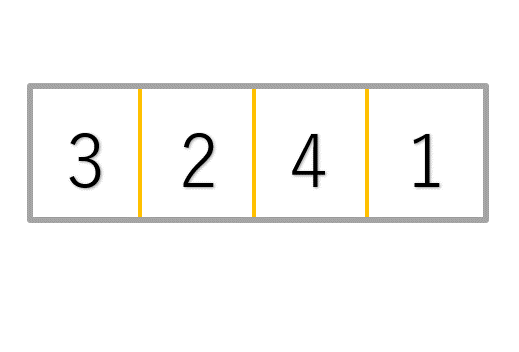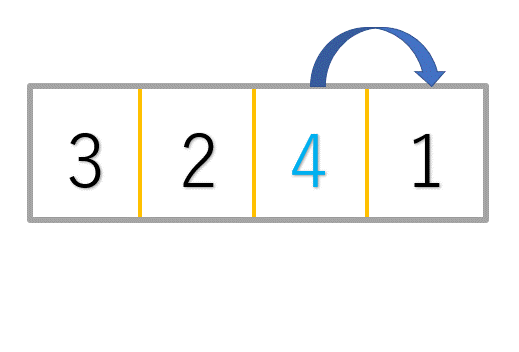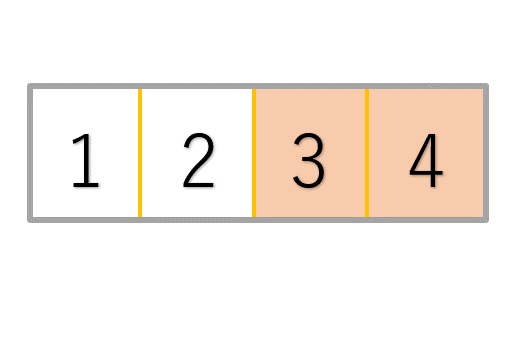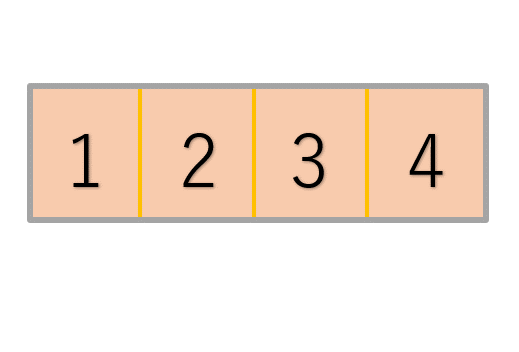
まずはイラストでイメージを確認しておきましょう。(見つかった最大値の候補を青色、整列済みのデータを赤色にしてあります)
上のイラストをみると、先頭からデータを確認していき(緑矢印)、その時点での最大値(青色)と比較して、より大きな値が見つかれば最大値を更新しているのが分かると思います。
基本挿入法では、こうして最後までデータを確認したうえで、最大値であるデータと末尾のデータを入れ替えてデータを整列させています。
それでは、基本選択法の比較回数はどうなるでしょうか?
1巡目では、最大値を調べるためにn-1回の比較を行っています。(その時点での最大値と比べて大きいかどうかを確認しています。)
2巡目は、末尾のデータが整列済みになっているのでn-2回...
最後は、先頭の値と2番目の値の比較のみで済むので1回の比較を行って終わりです。
ということで、先ほどの基本交換法と変わらず比較回数は(n-1)n/2になりますね。
つまりこれも重い処理になってしまっています。
基本挿入法について
基本挿入法では、データを整列済みのデータと未整列のデータに分けて考えます。
未整列の領域からデータを一つずつ取ってきて、整列済みのデータと大小関係を比較しながら正しい位置に挿入していけば、全てのデータを整列させることができます。
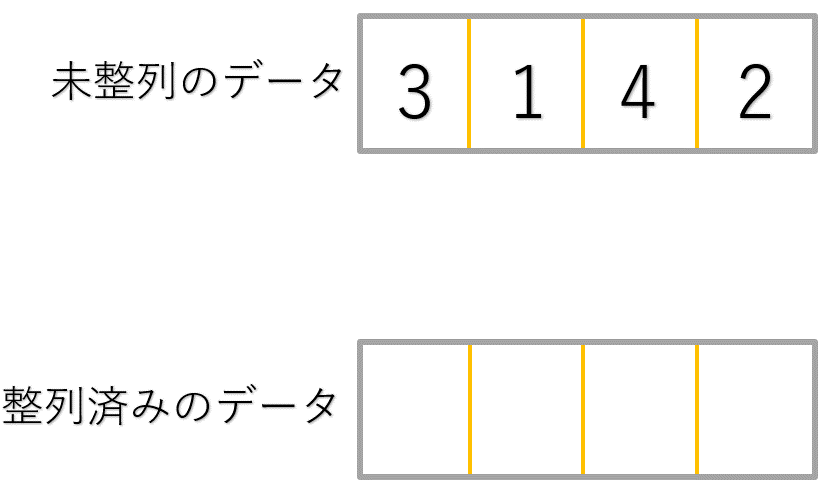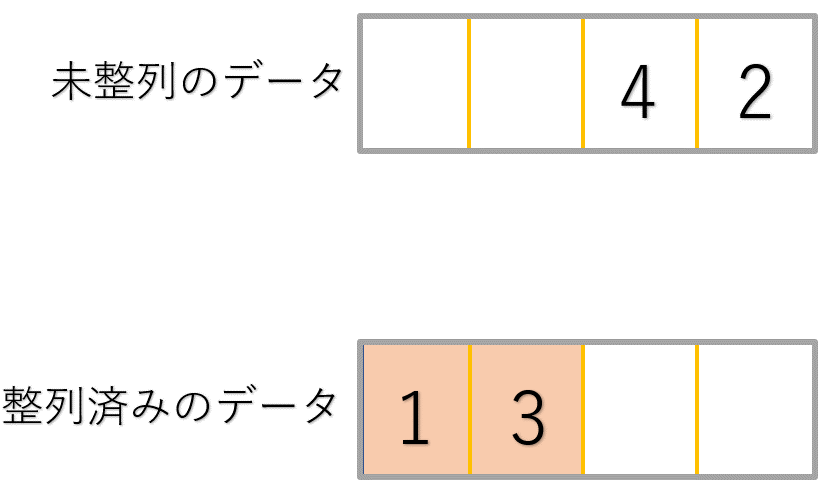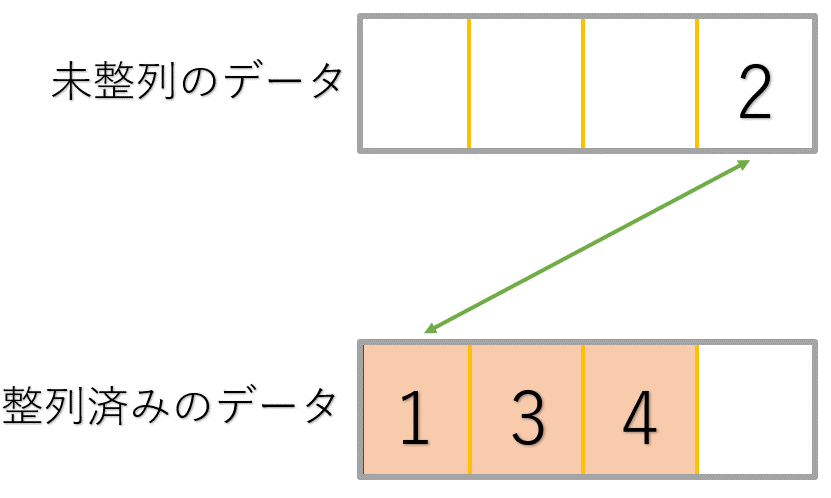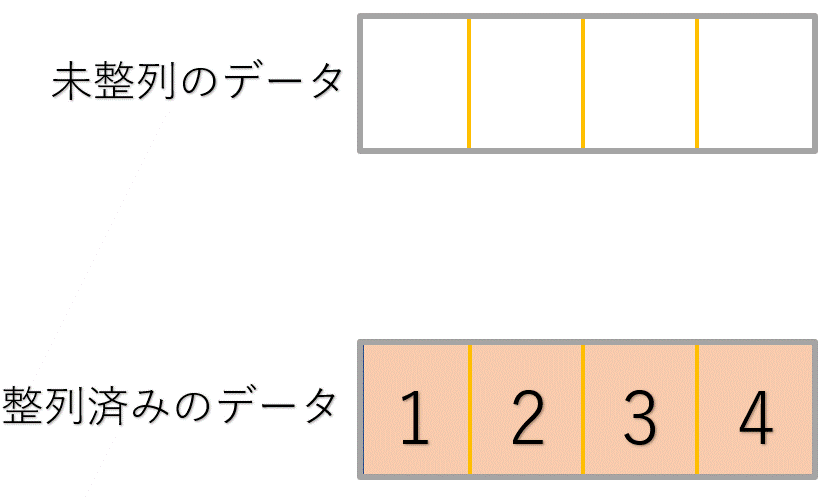
これも難しいので、まずはイラストでイメージを確認してみましょう。(最初のとっかかりとして、一番左に位置するデータを整列済みのデータとして考えます。)
イラストではそれぞれ以下のような手順に沿ってソートを行っています。
1巡目
①1と3を比較→3より小さいので3の左側に挿入
2巡目
①4と1の比較→1より大きいので次のデータと比較
②4と3の比較→3より大きいので3の右側に挿入
3巡目
①2と1の比較→1より大きいので次のデータと比較
②2と3の比較→3より小さいので1と3の間に挿入
このように、整列済みのデータと一つずつ比較を行って、正しい大小関係になるようにデータを挿入していくのが基本挿入法なんですね!
さて、この手順一覧を見て気づいたことがありますでしょうか?
よく見ると、3巡目の手順では、2と4の比較をすることなく挿入を行っています。
2は1よりも大きく3よりも小さいので、今回のケースのように挿入位置が確定してしまえばその時点で比較処理が終わります。
なので基本挿入法では元のデータの並びによっては比較回数が少なくて済みます。(並びが悪いと最大でn(n-1)/2回の比較が必要になります。)
これでデータの整列方法についての説明は終わりになります。
整列方法の良し悪しは比較回数だけでなく交換回数などにもよりますが、今回紹介した手法はどれも単純で効率が悪いものばかりです。
より素早くソートを行える高度な整列手法は、次回の記事で説明したいと思います。
まずはこの基本的な整列方法の流れを頭でイメージできるようにしておきましょう!
まとめ
- 基本交換法は隣り合うデータを比べてソートする
- 基本選択法は全体のデータから最大値(最小値)を抜き出して並べることでソートする
- 基本挿入法は未整列のデータからデータを抜き出して整列済みのデータの中に挿入していく
演習問題
1.基本交換法について誤っているものを選んでください。
A.隣接交換法とも呼ばれる。
B.バブルソートとも呼ばれる。
C.先頭と末尾のデータ同士を比べる。
2.データが次のようにソートされる場合、考えられるソート手法として最も適切なものを選んでください。
[6,8,4,2]→[6,2,4,8]→[4,2,6,8]→[2,4,6,8]
A.基本交換法
B.基本挿入法
C.基本選択法
3.基本交換法を使って次のデータをソートする場合に必要な比較回数を以下から選んでください。
[4,1,3,2]
A.4
B.5
C.6
D.7
答えは次回の記事で確認してください。
前回の演習問題~解答例
1.アルゴリズムに関する記述として最も正しいものを選んでください。
解答:B
解説:
A.順次処理に関する記述です。
B.正しい記述です。
C.選択(分岐)処理に関する記述です。
2.次のフローチャートの示すアルゴリズムの結果として最も正しいaの値を選んでください。
解答:B
解説:
初めに変数aに17が代入されています。
そのあと条件式による分岐処理が発生していますが、aを2で割った余りは1なので右側の処理が実行されます。
(a-1)/2の計算結果を求めると、8が答えになります。
3.次の疑似言語の示すアルゴリズムの結果として最も正しいNの値を選んでください
解答:D
解説:
初めに変数Nに-10が代入されています。
そのあと条件式による分岐処理が発生していますが、N<0は真なので「・N←-N」が実行され、Nに-(-10)、即ち10が代入されます。
次は後判定繰り返し処理が発生します。
現在Nの値は10ですが、条件式「N<0」の真偽を判定する前に「・N←-2N」が実行され、Nに-20が代入されます。
そのあと条件判定が行われますが、条件式「N<0」は真なのでもう一度同じ処理を繰り返します。
繰り返された処理の中でNには40が代入されますが、その後の条件判定では「N<0」が偽になり繰り返し処理は終了します。
よってプログラムが終了した時点でのNの値は40となります。