競技プログラミング風 C++問題集【第14回】

無向グラフ（難易度：★★★☆☆）

問題

複数の頂点と２つの頂点を結ぶ複数の辺から構成され、辺が両端の頂点から互いの相手の頂点に移動可能なものを「無向グラフ」と呼ぶ。

無向グラフの状態を表すクラスを UndirGraph とするとき、以下のメンバ関数を実装しなさい。

・頂点 v1 と v2 を引数にとり、それらの間に辺を追加する void addEdge(int v1, int v2)
・頂点 v1 と v2 を引数にとり、それらの間の距離を返す int dist(int v1, int v2)
・グラフが閉路を持つかどうかを返す bool hasCycle()

ただし、連結している頂点間距離はすべて1とする。
例えば、下図のような場合、v1, v2 間の距離は５となる。

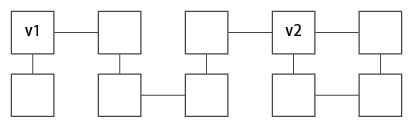
競技プログラミング風C＋＋問題集【第14回】_01

また、「閉路」とはある頂点から同じ頂点を２回以上訪れず、２つ以上の頂点を経由して元に戻ってくる経路（サイクルとも呼ばれる）のこととする。要するにループのことであり、上図のv2の右おより下部分が閉路である。

データ構造としては、vector<vector<int>> m_vertex; で、各頂点に連結している頂点リストを表すものとする。読者がこれ以外のデータ構造を用いたい場合は、変更してもかまわない。
[java] #include <iostream> // 標準入出力ライブラリ
#include <string>
#include <vector>
using namespace std; // std 名前空間使用
#define DO_TEST(exp) do_test(exp, __LINE__)
void do_test(bool b, int line) {
if( b ) return; // OK
cout << "\nNG at line " << line << "\n";
exit(1);
}
class UndirGraph {
public:
UndirGraph() {}
public:
string print() const {
string txt;
int i = 0;
for(const auto&lst: m_vertex) {
txt += to_string(i++) + ": ";
for(auto x: lst) {
txt += to_string(x) + ", ";
}
txt += "\n";
}
return txt;
}
void addEdge(int v1, int v2) { // 頂点 v1, v2 を連結, v1, v2 は 0 オリジン
// ToDo:
}
int dist(int v1, int v2) const { // 頂点 v1, v2 の距離を求める。非連結の場合は -1 を返す
// ToDo:
return 0;
}
bool hasCycle() const { // 巡回路があるか？
// ToDo:
return false;
}
private:
vector<vector<int>> m_vertex; // 頂点に連結している頂点リスト
};
int main() {
UndirGraph ug;
ug.addEdge(0, 1);
ug.addEdge(0, 4);
ug.addEdge(1, 2);
ug.addEdge(1, 3);
ug.addEdge(1, 4);
ug.addEdge(2, 3);
ug.addEdge(2, 5);
ug.addEdge(3, 4);
cout << ug.print();
//
DO_TEST( ug.dist(0, 1) == 1 );
DO_TEST( ug.dist(0, 2) == 2 );
DO_TEST( ug.dist(0, 3) == 2 );
DO_TEST( ug.dist(0, 4) == 1 );
DO_TEST( ug.dist(0, 5) == 3 );
DO_TEST( ug.dist(2, 4) == 2 );
//
DO_TEST( ug.hasCycle() );
if (1) {
UndirGraph ug;
ug.addEdge(0, 1);
ug.addEdge(0, 4);
ug.addEdge(1, 2);
ug.addEdge(3, 4);
DO_TEST(!ug.hasCycle());
}
if (1) {
UndirGraph ug;
ug.addEdge(0, 1);
ug.addEdge(1, 2);
ug.addEdge(2, 3);
ug.addEdge(3, 0);
DO_TEST(ug.hasCycle());
}
if (1) {
UndirGraph ug;
ug.addEdge(1, 2);
ug.addEdge(2, 3);
ug.addEdge(3, 1);
DO_TEST(ug.hasCycle());
}
cout << "\nGood Job!\n";
return 0;
}
[/java]

ヒント

・頂点v1と頂点v2を連結するには、m_vertex[v1] に v2 を追加するだけだ。
・ただし、重複チェックを忘れずに。
・また、本問題は無向グラフなので、v2 の連結リストに v1 を追加することも忘れずに。
・頂点間の距離を求めるには幅優先探索や反復深化アルゴリズムを用いるといいぞ。
・グラフにサイクル（閉路）があるかどうかを調べるには、探索済みフラグを更新しつつ深さ優先探索を行い、更新済み頂点に達した場合はサイクルがあると判定するといいぞ。

解答例

[java] void addEdgeSub(int v1, int v2) { // 頂点 v1 の連結リストに v2 を追加
if( find(m_vertex[v1].begin(), m_vertex[v1].end(), v2) == m_vertex[v1].end() )
m_vertex[v1].push_back(v2);
}
void addEdge(int v1, int v2) { // 頂点 v1, v2 を連結, v1, v2 は 0 オリジン
auto mxv = max(v1, v2);
if( (int)m_vertex.size() <= mxv )
m_vertex.resize(mxv+1);
addEdgeSub(v1, v2);
addEdgeSub(v2, v1);
}
int dist(int v1, int v2) const { // 頂点 v1, v2 の距離を求める。非連結の場合は -1 を返す
if( v1 < 0 || v1 >= (int)m_vertex.size() || v2 < 0 || v2 >= (int)m_vertex.size() )
return -1;
vector<int> dv(m_vertex.size(), -1); // 各頂点の v1 からの距離
int dst = dv[v1] = 0; // v1 からの距離
vector<int> lst; // 末端リスト
lst.push_back(v1);
bool found = false;
while( !found && !lst.empty() ) {
++dst;
vector<int> lst2; // 末端リスト
for(auto sx: lst) {
for(auto dx: m_vertex[sx]) {
if( dv[dx] < 0 ) { // 未探索
dv[dx] = dst;
if( dx == v2 ) {
found = true;
break;
}
lst2.push_back(dx);
}
}
if( found ) break;
}
lst.swap(lst2);
}
return dv[v2];
}
bool hasCycleDFS(vector<bool>& visit, int vx, int lstx) const {
visit[vx] = true;
for(auto dx: m_vertex[vx]) {
if( dx != lstx ) { // 直前に訪れた頂点でない場合
if( visit[dx] ) return true; // 巡回路あり
if( hasCycleDFS(visit, dx, vx) )
return true; // 巡回路あり
}
}
visit[vx] = false;
return false;
}
bool hasCycle() const { // 巡回路があるか？
vector<bool> visit(m_vertex.size(), false); // 探索済みフラグ
for(int i = 0; i != visit.size(); ++i) {
if( !visit[i] ) {
if( hasCycleDFS(visit, i, -1) )
return true;
}
}
return false;
}
[/java]

解説

頂点v1と頂点v2を連結するには、m_vertex[v1] に v2 を追加するだけだ。それを行う下請けが void addEdgeSub(int v1, int v2) だ。処理は簡単で、既に連結されていないかどうかをチェックし、連結されていなければ v2 を連結リストに追加するだけだ。
void addEdge(int v1, int v2) は、既にある頂点リスト配列要素数を超えていれば、配列サイズを拡張し、上記下請け関数を2回コールするだけだ。

頂点間の距離を求めるには幅優先探索や反復深化アルゴリズムを用いるとよい。解答例では幅優先探索を行っている。 vector lst; で末端リストを保持し、各末端リストの未訪問隣接頂点を lst2 に追加していき、最後に lst と lst2 を交換する。そして、未訪問隣接頂点が無くなるか v2 に達した時点で探索終了となる。

グラフにサイクルがあるかどうかを調べるには、探索済みフラグを更新しつつ深さ優先探索を行うとよい。更新済み頂点に達した場合はサイクルがあると判定する。また、独立した連結頂点群が複数ある場合に対応するために、サイクルが発見できなかった場合は、未探索頂点からサイクルがあるかどうか下請け関数を使って判定する。