競技プログラミング風 C++問題集【第7回】

数独（難易度：★★★☆☆）

問題

9×9の通常サイズの数独（「数独」は株式会社ニコリの登録商標です）の盤面情報を持つ１次元配列と、マス目位置（x, y）を引数で渡され、指定された箇所にどの数字が配置可能かを返す関数 short getCanPlacedNums(const short board[], int x, int y) を実装しなさい。

ただし、各マスの値は、空欄は0, 数値: 1を「数値-1」回左にシフトした値とする（1: 0x0001, 2: 0x0002, 3: 0x0004, 4: 0x0008, … 9: 0x0100）。
関数が返す値も上記のビット値のビット和とする。例えば、3と5が配置可能な場合は 0x0004 | 0x0010 = 0x0014 を返す。

また、x, y は 0 ～ 8 の範囲とし、左上が原点（0, 0）とする。

例えば、盤面が下図の場合、(2, 1) には、3, 5, 8, 9 を入れることができるので、getCanPlacedNums(board, 2, 1) は 0x0004 | 0x0010 | 0x0080 | 0x0100 = 0x0194 を返す。

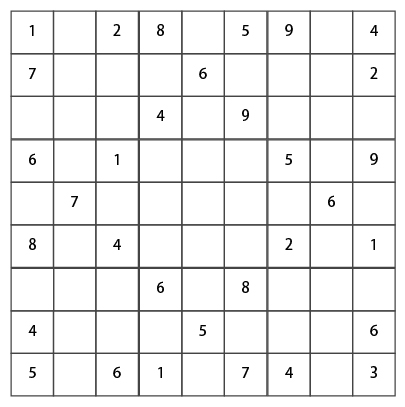
競技プログラミング風C＋＋問題集【第7回】_01

１次元配列中のデータの順序は、左から右、上から下の順序とする。

なお、知っている人がほとんだだとは思うが、念の為に数独ルールを以下に示しておく。

・各マスには数字 ‘1’～’9′ を入れる。
・横９マス・縦９マス・（上図の太線部分の）3×3ブロック内には同じ数字を入れない。
[java] #include <iostream> // 標準入出力ライブラリ
using namespace std; // std 名前空間使用
#define DO_TEST(exp) do_test(exp, __LINE__)
void do_test(bool b, int line) {
if( b ) return; // OK
cout << "\nNG at line " << line << "\n";
exit(1);
}
#define EMPTY 0
#define NUM_1 0x0001
#define NUM_2 0x0002
#define NUM_3 0x0004
#define NUM_4 0x0008
#define NUM_5 0x0010
#define NUM_6 0x0020
#define NUM_7 0x0040
#define NUM_8 0x0080
#define NUM_9 0x0100
#define WD 9
#define BWD (WD/3)
#define ALL ((1<<WD)-1)
void set(short* board, const char* ptr) {
for (; *ptr != ‘\0’; ++ptr)
*board++ = (*ptr >= ‘1’ && *ptr <= ‘9’) ? (1 << (*ptr – ‘1’)) : 0;
}
short getCanPlacedNums(const short board[], int x, int y) {
// ToDo: ここに str で指定された地形に貯まる水の面積を返すコードを記述
return 0;
}
int main() {
short board[WD*WD]; // 数独盤面
set(board, "1.28.59.47…6…2…4.9…6.1…5.9.7…..6.8.4…2.1…6.8…4…5…65.61.74.3");
DO_TEST( getCanPlacedNums(board, 0, 0) == 0 );
DO_TEST( getCanPlacedNums(board, 1, 1) == (NUM_3|NUM_4|NUM_5|NUM_8|NUM_9) );
DO_TEST( getCanPlacedNums(board, 2, 4) == (NUM_3|NUM_5|NUM_9) );
DO_TEST( getCanPlacedNums(board, 8, 4) == (NUM_8) );
cout << "\nGood Job!\n";
return 0;
}
[/java]

ヒント

・x, y 座標を1次元配列添字に変換するには x + y * WD とすればいいぞ。
・最初に (x, y) 位置に数字が入っているかどうかをチェックし、既に入っていれば 0 を返すんだぞ。
・配置済み数字をビット列で表す bits を用意し、これを 0 で初期化するぞ。
・x 列、y 行の各数字のビットを bits にビット論理加算（bits |= b）していく。
・3×3 ブロックについては、左上点をもとめ、そこから for文を2重に回し、各数字のビットを bits にビット論理加算していくといいぞ。
・関数が返すのは、使用済み数字ではなく使用可能数字なので、1～9 のビット部分を反転するといいぞ。

解答例

[java] short getCanPlacedNums(const short board[], int x, int y) {
if (board[x + y * WD] != EMPTY) return 0; // 空欄でない場合
short bits = 0; // 配置済み数字ビット
for (int i = 0; i != WD; ++i) // 縦横方向配について
bits |= board[i + y * WD] | board[x + i * WD]; // 配置済み数字ビット更新
int x0 = x – x % BWD; // 3×3ブロック左端位置
int y0 = y – y % BWD; // 3×3ブロック上端位置
for (int v = 0; v != BWD; ++v) { // 3×3ブロック内の各位置について
for (int h = 0; h != BWD; ++h)
bits |= board[x0 + h + (y0 + v) * WD]; // ブロック内数字配置済み数字ビット更新
}
return ALL ^ bits; // 配置済み数字を反転することで配置可能数字ビットを返す
}
[/java]

解説

x, y 座標を配列添字に変換するには x + y * WD とするとよい。なので、最初に board[x + y * WD] が空欄（EMPTY）かどうかをチェックし、空欄でなければ数値を配置できないので 0 を返す。
次に、縦・横・3×3ブロック内に配置済み数字をビット列で表す bits を用意し、これを 0 で初期化しておく。 3 が配置済みであれば 0x004 を、4 が配置済みであれば 0x008 のビットが立っているものとする。したがって、配置済みビットが 0x00c であれば、数字3と4が配置済みであることを表す。ビット演算に慣れていない人にはちょっと難しいことかもしれないが、ビット列を使えば、このように複数の状態をひとつの変数で表すことが可能になり、メモリ効率・実行効率ともに優れたものになる。
次にfor文で行・列を回して、縦横方向のマスで使用している数字のビットを bits に論理加算する（bits |= board[ix]）。通常の加算であれば、同じ数字を2回加えると値が倍になってしまうが、論理加算であれば何回加算しても、そのビットにしか影響を与えない。
getCanPlacedNums() 関数は配置可能なビット列を返さないといけないが、bits には使用済みビット列が入っているので、 1～9 のビット部分を反転する必要がある。そのためには ALL ^ bits を返せばよい。これは、反転したいビット部分が1の値と排他的論理和（XOR）を取ると、その部分だけ反転するというテクニックだ。