StringSearch～文字列検索アルゴリズム～【中編】

目次

• BMH
• – 大文字小文字同一視
• – パフォーマンス計測

前回は力まかせ（ブルートフォース）探索について解説した。
今回は、それを高速化したアルゴリズムのひとつであるBMH法について解説する。

BMH（Boyer–Moore–Horspool）アルゴリズム

本章では、前章で示した検索関数の高速化に挑戦してみる。
検索は検索パターンを被検索文字列と順に比較していく単純な処理なので、
高速化は困難だと思われる方も少なくないだろう。
だが実は、パターンを前処理しておくことでスキップ量を増やし高速化することが可能なのだ。

具体的には、パターンが被検索文字列にマッチしない場合に、常に１文字進めるのではなく、
パータンそのものと不一致になった部分の情報を利用することで、
可能な限り比較場所を進め、高速化するというアルゴリズムだ。

下図にその具体例を示す。

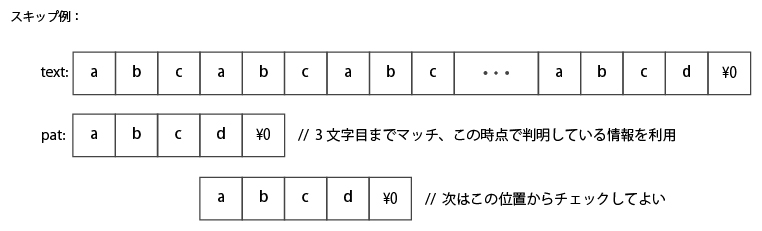
この類で最初期のものは「Knuth–Morris–Pratt アルゴリズム（1977、以下 KMP法と略す）」だ。
力まかせ探索アルゴリズムがいつから使われていたのかははっきりしないが、
コンピュータが使われだした最初期からだと考えらるので、1950年代後半には使われていたものと推測される。
つまり、約20年もかかってやっと検索アルゴリズム高速化方法が考えだされたということだ。
だが、高速化が可能だとわかると、それにインスパイアされて様々なアルゴリズムが提案されるようになった。

KMP法のアルゴリズムは比較的複雑で解説が大変なので、本稿では具体的なコードの説明は行わない。
代わりに比較的単純で高速な Boyer–Moore–Horspool アルゴリズム（1980, 以下 BMH法と略す）について解説する。

KMP法では不一致の時に、利用可能な情報をできるだけ利用するので、スキップ量は多くなる傾向にあるが、
その処理に時間を要するので、トータルで高速になるとは限らない。
それに対してBMH法は、不一致のときにパターン最後の文字に対応する位置の文字だけに着目する。
処理が非常に単純になるので、スキップ量を求める処理が高速で、KMP法に比べてスキップ量も遜色ないので、
スキップ量を増やす類のものの中では最も高速なアルゴリズムのひとつだと言われている。

下図にBMH法によるスキップの具体例を示す。

BMH法ではパターン末尾の方から比較し、不一致の場合はパターン末尾位置の被検索文字にのみ着目する。
上図ではパターン末尾位置の被検索文字の ‘x’ に着目する。
この場合、’x’ は検索パターンに含まれておらず、パターンを 1～3文字ずらしてもマッチしないのは明らかなので、
比較位置をパターン長の4文字分スキップ可能というわけだ。

以下、BMH法で不一致になった場合の、スキップケースをいくつか上げておく。

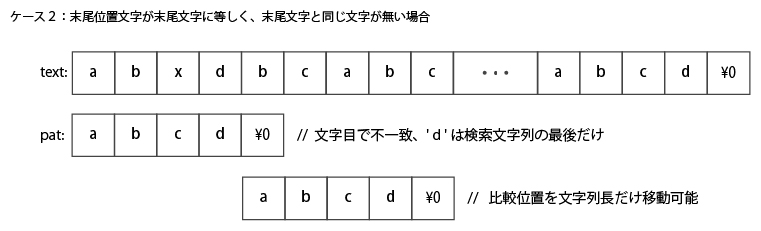
上記は、末尾位置文字が末尾文字に等しく、末尾文字と同じ文字が無い場合。
この場合も、パターンをパターン長未満ずらしても一致することはありえないので、パターン長だけずらすことができる。

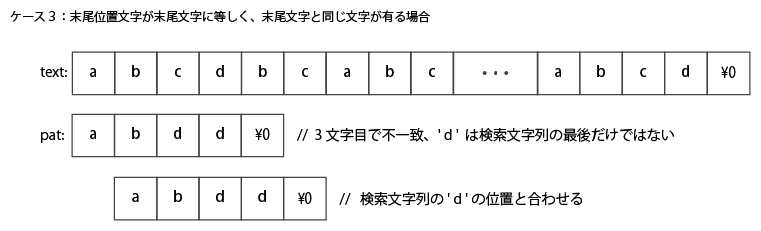
上記は、末尾位置文字が末尾文字に等しく、末尾文字と同じ文字が有る場合。
末尾文字と同じ文字の位置をあわせるて比較する必要があるので、この場合は１文字だけずらす。

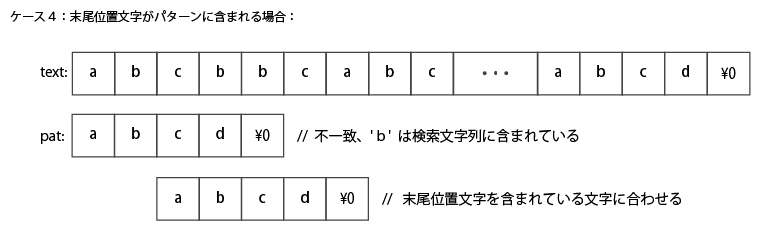
上記は末尾位置文字がパターンに（１つだけ）含まれる場合。
この場合も、末尾文字と同じ文字の位置をあわせるて比較するようにスキップする。

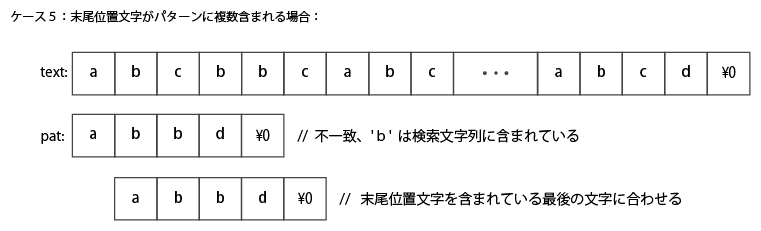
最後のケースは、末尾位置文字がパターンに（ひとつではなく）複数含まれる場合。
この場合はパターンの最後に出現する位置に末尾位置文字をあわせるように比較位置をスキップする。

以上を踏まえると、BMHのコードは以下のように記述できる。

cchar* strstrBMH(cchar* text, cchar *pat)
{
    const int plen = strlen(pat);
    while( *text != '\0' ) {    //  text が末尾まで達していない間
        if( startsWithBkw(text, g_pat, plen) )      //  検索パーンと一致するか？（大文字小文字同区別）
            return text;                //  一致すれば一致アドレスを返す
        //  不一致の場合、text[plen-1] を、pat[plen-2] から前方向に検索し、
        //  最後の位置からの差だけ、text を進める
        int ix = plen - 1;
        while( --ix >= 0 ) {
            if( pat[ix] == text[plen-1] )
                break;
        }
        if( ix < 0 )
            text += plen;   //  末尾位置文字が含まれなかった場合
        else
            text += plen - ix;  //  末尾位置文字が含まれていた場合
    }
}

処理内容はコメントに書いている通り。
上記コードで比較箇所を飛ばし飛ばしできるので、最良の場合の処理速度は O(N/M) になるのだが、
パターン末尾位置に対応する文字を調べ、どれだけスキップ可能かを決める処理に時間を要している。
この量はパターンにのみ依存して文字ごとに決まるので、あらかじめ各文字ごとの移動量を計算し、
配列に保存しておき、検索時にはそれを参照するようにするととで、はるかに処理を高速化できる。

なお、テキストとパターンを末尾から比較する関数は以下のように定義できる。

bool startsWithBkw(cchar* text, cchar* pat, int plen)       //  末尾からｎ文字比較
{
    while( --plen >= 0 ) {
        if( text[plen] != pat[plen] )
            return false;       //  不一致
    }
    return true;    //  一致
}

検索処理を高速化するため、実際に検索を行う前に、前処理として検索パターンの各文字を調べ、
その文字が検索パターン末尾位置に存在したときのスキップ量をテーブル化する。
下記に前処理のコードを示す。

int g_plen;         //  検索文字列長
cchar* g_pat;       //  検索文字列
int g_BMH[256];     //  スキップテーブル
bool setupBMH(cchar* pat)
{
    g_plen = strlen(g_pat = pat);   
    for(auto& x: g_BMH) x = g_plen; //  テーブル要素をすべて検索文字列長に設定
    for(int i = 0; i != g_plen - 1; ++i)        //  パターンの先頭文字から末尾のひとつ前の文字までループ
        g_BMH[(uchar)*pat++] = g_plen - i - 1;      //  文字 *pat で不一致になった場合のスキップ可能長
    return true;
}

例えば検索パターン「abac」で上記関数を実行すると、g_BMH[] の値は以下のようになる。

g_BMH[‘a’] = 1, g_BMH[‘b’] = 2, g_BMH[‘c’] = 4, g_BMH[‘a’～’c’以外の文字] = 4

各文字ごとのスキップ量が g_BMH[] に計算済みの場合、BMH法検索関数は以下のように記述できる。

cchar* strstrBMH(cchar* text, cchar *endptr)
{
    while( text + g_plen <= endptr ) {  //  検索パターン分の文字列が残っている間ループ
        if( startsWithBkw(text, g_pat, g_plen) )        //  検索パーンと一致するか？（大文字小文字同区別）
            return text;                //  一致すれば一致アドレスを返す
        text += g_BMH[(uchar)text[g_plen-1]];   //  スキップテーブルの値だけ、text を進める
    }
    return nullptr;
}

これで、最良処理時間 O(N/M) のかなり高速な関数が出来上がった。
実際の処理時間は後で示す。

◎ 大文字小文字同一視

次に大文字小文字同一視の場合を示そう。

bool setupIcBMH(cchar* pat)     //  大文字小文字同一視版
{
    if( !(g_plen = strlen(g_pat = pat)) )
        return false;       //  検索文字列が空の場合
    for(auto& x: g_BMH) x = g_plen; //  テーブル要素をすべて検索文字列長に設定
    for(int i = 0; i != g_plen - 1; ++i) {
        uchar ch = *pat++;
        g_BMH[tolower(ch)] = g_BMH[toupper(ch)] = g_plen - i - 1;       //  文字 *pat でのスキップ可能長
    }
    return true;
}

大文字小文字を同一視するには、strcasestr() の場合同様に、比較の時に文字の大文字小文字同一視するだけでなく、
各文字を大文字・小文字変換した文字について、g_BMH[] テーブルを作成するとよい。

cchar* strcasestrBMH(cchar* text, cchar *endptr)
{
    while( text + g_plen <= endptr ) {  //  検索パターン分の文字列が残っている間ループ
        if( startsWithIcBkw(text, g_pat, g_plen) )        //  検索パーンと一致するか？（大文字小文字同一視）
            return text;                //  一致すれば一致アドレスを返す
        text += g_BMH[(uchar)text[g_plen-1]];   //  スキップテーブルの値だけ、text を進める
    }
    return nullptr;
}

文字列比較は startsWithBkw() ではなく、大文字小文字同一視で比較する startsWithIcBkw() を用いる。
その定義は startsWithIc() とほぼ同じなので、本稿では省略する。
具体的なコードは github を参照してほしい。

◎ パフォーマンス計測

被検索文字列、検索パターンともに ‘a’-‘z’ のランダム、
被検索文字列長は100メガ（1億）で、検索パターンを 10文字、20文字と長くした場合の処理時間を計測してみる。

計測結果（環境：Core i7-6700 3GHz, 32GB, Windows 10）：

検索パターン長を長くした場合の検索に要した時間（単位ミリ秒）：

アルゴリズム	5	10	20
my_strstr	151	102	103
my_strstr2	64	61	79
my_strcasestr	537	577	578
BMH	72	74	27
BMH_IC	88	48	31

BMH法は、大文字小文字区別：my_strstr2() と同程度の速度だ。
力まかせ法は O(N*M) だったのに対し、BMH法はおおむね O(N/M) となっているのがわかる。
また、大文字小文字を同一視する my_strcasestr() はかなり低速になったが、
BMH法の場合はほとんど低速化しないのがわかる。

課題：
・BMH法ではパターン末尾位置の１文字だけを利用し比較位置をスキップするが、
　末尾から２文字を利用する検索関数を実装・パフォーマンス計測してみなさい。

筆者：津田伸秀 プロフィール：テニス・オセロ・ボードゲーム・パズル類が趣味の年齢不詳のおじさん。 自宅研究員（主席）。vi と C++が好き。迷走中・・・ ボードゲーム・パズル系アプリ開発・リリースしてます。