【C++】ナンバーリンク【前編】

目次

• はじめに
• ナンバーリンク
• ソルバー
• L データ構造
• L ブルートフォース
• L バックトラッキング

はじめに

ナンバーリンク

ナンバーリンクとは WxH の矩形盤面に１～Nまでの数字をそれぞれ２個ずつ配置し、
全部のセルを埋めて、縦横方向だけ（斜め線不可）で同じ数字をつなげるというパズルだ。
下図に、4×4 盤面に１～３を配置する問題の一例を示す。

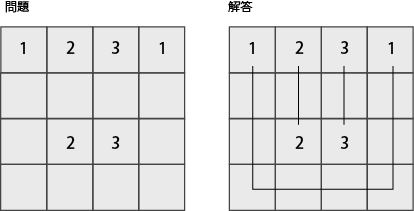
解答に空きがあってもよいなど細かいルールの種類がいくつかあるが、
本稿では全部のセルを埋めるものとする（下図参照）。

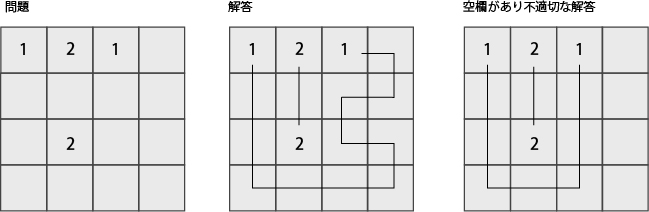
下図のように数字とつながらないループがある場合も不適切とする。
このような短絡ループは関西解と呼ばれることがある（下図参照）。

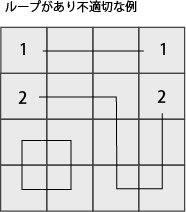
数字ではなく、Flow等の様に同じ色や数字をつなげるものもある。

ナンバーリンクは制約充足問題の一種であり、複数の解があるものは不適切な問題と呼ばれる。
オリジナルは「Numberlink」で1910年代に考案されたようだ。
※ なお、「ナンバーリンク」は株式会社ニコリの登録商標だ。

ソルバー

◎ データ構造

まず、ソルバーで使用するデータ構造について説明する。

各セルの数字は m_number[] 配列で保持される。
値が0なら空欄で、1以上なら数字が配置されていることを表す。
盤面は２次元だが、処理の高速化のために１次元とする。
上下右にひとマス大きい１次元配列で、盤面外の部分には番人（値：-1）を入れておく。
番人はよく使用される高速化テクニックで、値を見るだけで添字範囲チェックを省略することができる。
左右セルは ix-1, ix+1、上下セルは ix-配列幅, ix+配列幅 で参照することができる。
（本稿のコードでは配列幅に m_aryWidth というメンバ変数を割り当てている）
4×4 の場合の盤面配列を下図に示す。数字はそのセルのインデックスだ。
下図に盤面配列のインデックス値を示す。左上は5、右上は8, 右下は23となる。

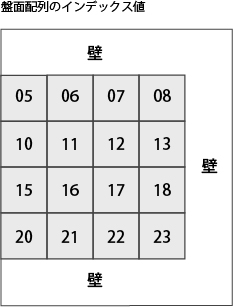
問題の空欄には ━ ┃ ┏ ┓ ┗ ┛ の6種類のリンクが入る可能性がある。
数字のあるセルは上下左右連結の4種類の可能性がある。
各セルがどの方向に連結しているかは m_linkRt[], m_linkDn[] 配列で情報を保持する。
ix から右に連結している場合 m_linkRt[ix] = true、連結していなければ false だ。
ix から下に連結している場合 m_linkDn[ix+配列幅] = true、連結していなければ false だ。
情報の二重化を防ぐために、右から左、下から上への連結情報は保持しない。

m_number[] と m_linkRt[], m_linkDn[] で状態を完全に指定できるので、これだけで解を探索可能だ。
が、数字がつながっているか・空ループがないかなどをチェックするにはリンクをたどる必要があり、
それに少々時間を要する。そこで、それを高速化するために mate[] 配列というものを導入する。
毎回ある程度重い処理を行うより、予め前処理をしておいた方がトータルで高速になるというテクニックだ。
Nクィーンの時に用いた配置フラグと同じような意味だ。
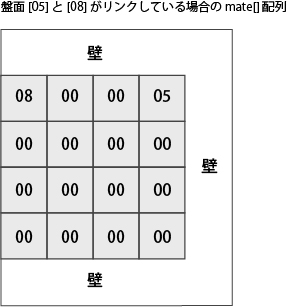
mate[ix] は、ix セルにリンクしている逆側セルのインデックスを保持する。
例えば盤面左上と右上がリンクしている場合は下図のようになる。

◎ ブルートフォース

ブルートフォース（力まかせ）探索とは、空欄を全部埋めて、解になっているかをチェックするというアルゴリズムだ。
これで解を求めることは理論的には可能だが、処理時間がかかりすぎて盤面が非常に小さいサイズでない限り実用的ではない。
なので、具体的なコードは省略する。

・課題：

◎ バックトラッキング

バックトラッキング探索とは、解として不適切と判明した時点で後戻りを行う（これを枝刈りと呼ぶ）アルゴリズムだ。
不要な探索を行わずに済む分、ブルートフォースより高速になる。
ただし、解として不適切かどうかの判定に時間をかけすぎるとかえって遅くなることもある。
一般的には探索の根本に近いほど枝刈りの効果が大きいので、多くの時間をかけてもよく、
末端に近い場合は解として不適切かどうかを判定するより、末端まで探索した方が高速になることもある。

本稿では、そのような判定は行わず、
・数字がある場所へのリンクはひとつだけか？
・同じ数字とリンクしているか？
を常にチェックし、そうでなければ枝刈りを行うようにした。
その結果、ブルートフォースに比べると極めて高速で
10×10 の問題を１秒未満で解くことが出来るようになった。

後編にて、ナンバーリンクソルバーの具体的なコードについて解説する。

筆者：津田伸秀 プロフィール：テニス・オセロ・ボードゲーム・パズル類が趣味の年齢不詳のおじさん。 自宅研究員（主席）。vi と C++が好き。迷走中・・・ ボードゲーム・パズル系アプリ開発・リリースしてます。