アルゴリズム(承前)
前編・中編で4×4オセロの完全解析を行うために、ビットボードというデータ構造と、
ビット演算を用いてビット数を高速にカウント・反転処理などのためのアルゴリズムを解説した。
本稿では、ビットボードを使ったアルゴリズムとして、完全解析を行うための深さ優先探索、および解析結果を解説する。
深さ優先探索
ゲーム木探索は、大きく言うと、深さ優先探索と幅優先探索の2種類がある。
深さ優先探索とは、先へ先へと局面を進めていき、末端に到達したらひとつ前に戻って、
次の手を探索するというアルゴリズムだ。
単純で高速なので、ゲーム木が小さく全探索可能であればこれで充分だ。
下記は深さ優先探索で全局面を探索し、双方最善手を打った場合の石数差を返すものだ。
双方最善という仮定で読み進めていくので、末端評価を常に黒から見た石数差だとすれば、
黒番では次のノードの最大値を、白番では最小値をそのノードの評価値として返す。
だが、そうすると白黒でコードを2つ書かなくてはいけないので、白番のときは白黒
を交換し、同じ negaMAx() をコールしている。
このように、白黒交換が非常に簡単で、ほぼコスト0で可能なのもビットボードの利点のひとつだ。
int negaMax(ushort black, ushort white)
{
if( 末端局面 )
return numOfBits(black) - numOfBits(white);
int maxVal = INT_MIN;
foreach(p すべての空欄) {
ushort rev = get_rev(black, white, p); // 反転パターン取得
if( rev != 0 ) { // 石が返る場合
doPut(black, white, p, rev); // 石を返す
int v = -negaMax(white, black); // 白黒反転して自分自身を再帰コール
if( v > maxVal ) max = v;
doPut(black, white, p, rev); // 反転した石を戻す
}
}
return maxVal;
}
自分自身をコールする部分は以下のように最適化することもできる。
そうすれば、状態を元に戻す必要すらない。
.....
if( rev != 0 ) { // 石が返る場合
// 白黒反転して自分自身を再帰コール
int v = -negaMax(white ^ rev, black ^ rev ^ p);
if( v > maxVal ) max = v;
}
.....
実は、上記コードは打つ箇所が無くてパスになった場合に対応していない。
以下に、パスに対応したコードを示す。
なお、双方パスになった場合は終局となるが、その場合、空欄部分は勝者のものと
なるよう2014年にルールが変更されているので、それにも対応している。
int negaMax(ushort black, ushort white, int nspc, bool pass) // 黒番深さ優先探索
{
if( nspc == 0 ) {
return numOfBits(black) - numOfBits(white);
}
ushort space = ~(black | white); // 空欄の部分だけビットを立てる
int maxev = -9999;
bool put = false;
while( space != 0 ) {
const ushort p = space & -space; // 一番右のビットのみ取り出す
ushort rev = getRev(black, white, p); // 反転パターン取得
if( rev != 0 ) { // 石が返る場合
int ev = -negaMax(white^rev, black|p|rev, nspc-1, false);
maxev = max(maxev, ev);
put = true;
}
space ^= p; // 一番右のビットをOFFにする
}
if( put ) // パスでない場合
return maxev;
if( pass ) { // 白黒双方がパスの場合
//maxev = numOfBits(black) - numOfBits(white); // 2014年以前の日本ルール
// 2014年以降の新ルール
const auto nb = numOfBits(black);
const auto nw = numOfBits(white);
maxev = nb - nw;
if( nb > nw ) maxev += nspc;
else if( nb < nw ) maxev -= nspc;
return maxev;
} else
return -negaMax(white, black, nspc, true);;
}
課題
全局面を調査するのではなく、双方最善の場合の石数差のみを求めるのであれば
アルファベータ探索を行って、処理時間を短縮することができる。アルファベータ関数
またはネガアルファ関数を実装し、動作確認・処理時間比較をしてみなさい。
置換表(トランスポジションテーブル)
ある局面から、着手A, B, C と 着手C, B, A の様な場合に、異なる手順で同一局面になることがある。
このような場合に、同一局面を再度探索しないよう、局面を置換表に登録して回避し
探索局面を減らすことできる。
将棋やチェスの場合は、コマの種類、位置に乱数を割り当て、それらの排他的論理和をハッシュキー
とすることが多いが、 4×4オセロでビットボードを用いる場合、32ビット数値で局面を表現できるので、
32ビット数値をそのままハッシュキーに用いることができる。
本稿では下リストの様に std::unordered_map を利用した。局面の登録・検索は同クラスのメソッド・
演算子を利用する。
局面は (black<<16) | white をキーとし、手番は黒番固定とする。
同一局面の白番は白黒を入れ替え((white<<16) | black がキー)て登録する。
std::unordered_map<uint, char> g_tt; // 局面→石差 トランスポジションテーブル
g_tt[makeUint(black, white)] = v; // 局面・石差を登録
g_tt.find(makeUint(black, white)) // 局面登録チェック
置換表を用いたネガマックス関数のコードを以下に示す。
// 黒番深さ優先探索、トランスポジションテーブル使用版
int negaMaxTT(bitboard_t black, bitboard_t white, int nspc, bool pass)
{
uint32 key = (black<<16) | white;
auto itr = g_tt.find(key); // 局面がトランスポジションテーブルに登録されているかチェック
if( itr != g_tt.end() ) // 登録済みの場合
return itr->second;
if( nspc == 0 ) {
//cout << boardText(black, white) << "\n";
auto v = numOfBits(black) - numOfBits(white);
g_tt[key] = v; // トランスポジションテーブルに追加
g_tt[(white<<16) | black] = -v; // 白の手番であっても終局なので、白黒反転も追加
return v;
}
.....
if( put ) { // パスでない場合
//return maxev;
} else if( pass ) { // 白黒双方がパスの場合
//maxev = numOfBits(black) - numOfBits(white); // 2014年以前の日本ルール
// 2014年以降の新ルール
const auto nb = numOfBits(black);
const auto nw = numOfBits(white);
maxev = nb - nw;
if( nb > nw ) maxev += nspc;
else if( nb < nw ) maxev -= nspc;
} else {
maxev = -negaMaxTT(white, black, nspc, true);;
}
g_tt[key] = maxev; // 探索結果をトランスポジションテーブルに追加
return maxev;
}
完全解析結果
以下に本プログラムで計算した双方最善手順を示す。
初手はどこに打っても対称なので、d3 に打つものとした。
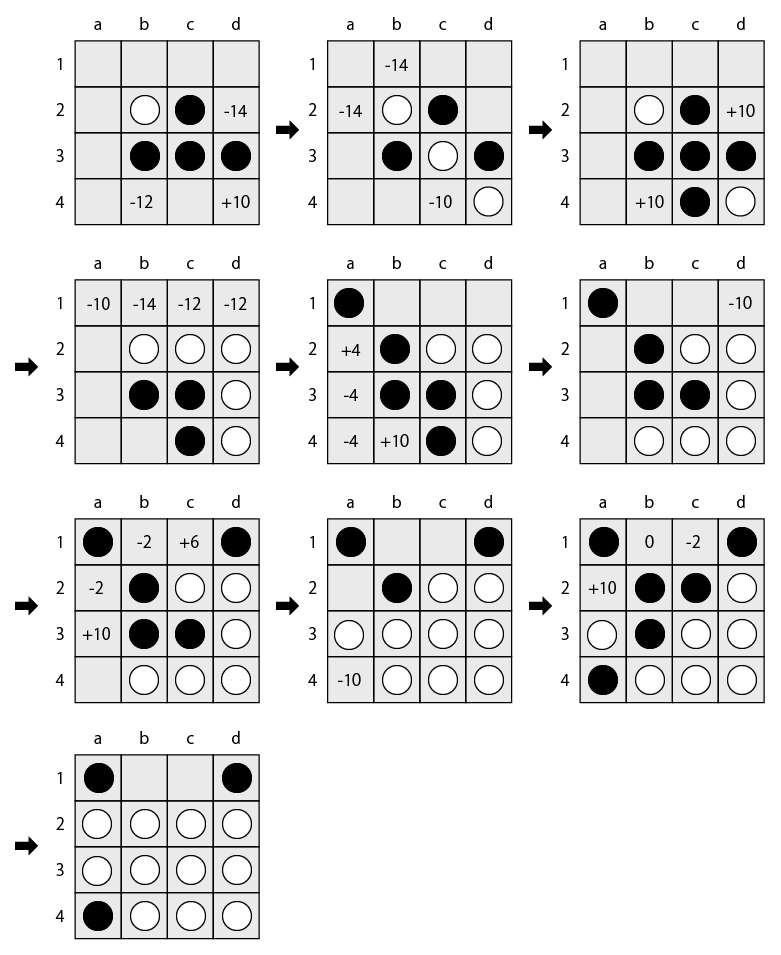
2手目白は斜めが最善。4×4オセロでも序盤に角を取るのは有利なようだ。
5手目は「たぬき定石」というか黒も角を取るが、このあと白は意図的に相手に角を取らせる
有段者的打ち回しで、辺・中心部分を確定させ、2個空きで終局。黒3、白11個だが、残った
空欄は勝者のものなので、白の (11+2)-3 = 10石勝ちとなる。
最後に
データ構造としてビットボードを使用し、深さ優先探索で4×4オセロを完全解析するための
アルゴリズムについて解説した。ビット演算に馴染みがない人にはちょっと難しかった
かもしれないが、有効なプログラミングテクニックなのでぜひマスターしてただきたい。
NxNの盤面で各マスの状態数が限られている場合は、状態をビットで表すことで、
無条件分岐・演算並列化により高速化できる場合があるので、ビットボードを利用できないか
検討してみるといいかもしれない。
課題
4×6, 4×8, 6×6 オセロの完全解析に挑戦してみなさい
関連記事
投稿が見つかりません。
 |
筆者:津田伸秀 プロフィール:テニス・オセロ・ボードゲーム・パズル類が趣味の年齢不詳のおじさん。 自宅研究員(主席)。vi と C++が好き。迷走中・・・ ボードゲーム・パズル系アプリ開発・リリースしてます。 |




