4×4 オセロ完全解析【第2回】

TsudaNobuhide

アルゴリズム（承前）

前編では4×4オセロの完全解析を行うために、ビットボードというデータ構造と、
ビット演算を用いてビット数を高速にカウントするアルゴリズムなどを解説した。

引き続き本稿では、ビットボードを使い石を高速に反転するアルゴリズムなどを解説していく。

すべての空欄に対する処理

オセロのゲーム木探索においてはすべての空欄に対する処理が必要だ。
普通にループで書くと以下のようになる。ループ回数は常に16回となる。

    ushort space = ~(black | white);    //  空欄の部分だけビットを立てる
    for(ushort p = 0x8000; p != 0; p >>= 1) {   //  各ビットについて
        if( (p & space) == 0 ) continue;        //  空欄でなければ次のビットへ
        //  すべての空欄に対する処理
        .....
    }

-x = ~x + 1 なので、下図の様に x & -x で一番右のビット１だけを取り出すことができる（x が0の場合は0を返す）。

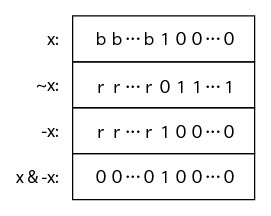
4x4 オセロ完全解析【第2回】

この演算を使えば、すべての空欄に対する処理は以下のように記述できる。
ループはビットボード全体のビット数ではなく、ちょうど空欄の数だけ回る。

    ushort space = ~(black | white);    //  空欄の部分だけビットを立てる
    while( space != 0 ) {
        ushort p = space & -space;      //  一番右のビットのみ取り出す
        //  空欄 p に対する処理
        .....
        space ^= p;                     //  一番右のビットをOFFにする
    }

石を反転する処理

黒石を置く位置を p、それにより反転するパターンを rev とすれば、
黒石を置いて白石を反転させる処理は以下のように記述できる。
ex-or（排他的論理和）で演算しているので、この処理は可逆的で、
2回コールすると盤面の状態が元に戻るというのも面白いところだ。

void doPut(  ushort &black,      //  黒石
                    ushort &white,      //  白石
                    ushort p,           //  黒石を置く位置
                    ushort rev)         //  反転するビットパターン（計算方法は次節参照）
{
    black ^= p | rev;
    white ^= rev;
}

反転するパターンをどうやって計算するのかと思われるかもしれないが、その説明は次節で行う。

反転する石を計算

「・○●」と「・○○●」の場合のみチェックすればよい。

「・○●」の中央の白石に注目すると、左が黒着手位置の空欄 & 中央が白石 & 右側が黒石
であれば白石が反転することになるので、着手位置を p、その部分が空白とすると
(p >>1) & white & (black<<1) で中央白石が反転するかどうかを取得できる。水平方向に白石が返る可能性があるのは中央部分だけなので、あらかじめ ushort wh = white & 0x6666; で反転可能マスクパターンを作っておけば、 (p >> 1) & wh & (black << 1) で反転可能位置パターンを取得できる。
この反転可能位置パターンにより、シフトによるオーバーフローも自動的に対処できる。

「・○○●」のように2箇所が返る場合も同様に処理できる。ただし返る石の位置毎に
2回同じような処理を行っている。この部分はもう少し最適化（論理演算を減らすことが）
可能な気がする。

それにしても、なかなか美しいアルゴリズムだと思わないだろうか？
筆者が初めてこのアルゴリズムを知ったときは、なるほどこんな方法もあるのかと、
ビットボードの有効性にかなりの衝撃を受けたものだ。

全体のコードは以下のようになる。

ushort getRev(ushort black, ushort white, ushort p)     //  黒を p に打った場合に、反転する白のパターンを取得
{
    if( ((black | white) & p) != 0 ) return 0;      //  p が空白ではない場合
    ushort rev = 0;                         //  反転パターン
    const ushort wh = white & 0x6666;           //  水平方向用マスク
    //  右方向に返る石をチェック
    rev |= (p >> 1) & wh & (black << 1);    //  ・○● の場合
    rev |= (p >> 1) & wh & (wh << 1) & (black << 2);    //  ・○○● の場合の空欄隣の○
    rev |= (p >> 2) & (wh >> 1) & wh & (black << 1);    //  ・○○● の場合の次の○
    //  左方向に返る石をチェック
    rev |= (p << 1) & wh & (black >> 1);    //  ●○・ の場合
    rev |= (p << 1) & wh & (wh >> 1) & (black >> 2);    //  ●○○・ の場合の空欄隣の○
    rev |= (p << 2) & (wh << 1) & wh & (black >> 1);    //  ●○○・ の場合の次の○
    //
    const ushort wv = white & 0x0ff0;           //  垂直方向用マスク
    //  上下方向に返る石をチェック
    .....
    const ushort wd = white & 0x0660;           //  斜め方向用マスク
    //  斜め４方向に返る石をチェック
    .....
    return rev;
}