ITを学ぶなら
｢テックプロジン｣

Developer

4×4 オセロ完全解析【第1回】
2020.03.09
Lv3

4×4 オセロ完全解析【第1回】

TsudaNobuhide

はじめに

本稿では、データ構造にビットボードを用い、4×4サイズのオセロ[*1]の完全解析を行うためのアルゴリズムについて前中後編に分けて解説する。
*1 「オセロ」「Othello」は株式会社メガハウスの登録商標

「完全解析」とは、初期局面からゲームルールに従って到達可能な全局面を調査し、双方が常に最善手を打つと仮定して、それら全ての勝ち負けを決定することである。要するに、ゲームのすべてを調査しつくすということだ。
最初にビットボードというデータ構造について説明し、ついで、完全解析を行うためのアルゴリズムについて解説する。
なお、完全解析を行うプロジェクトは github（https://github.com/vivisuke/Othello4x4）
で公開しているので、コード全体を読みたい・実際に実行して試してみたい人は参照されたい。

ビットボード

「ビットボード」とは、盤面の白石・黒石の状態をそれぞれのビット値で表すデータ構造だ。
通常の配列を使う場合は、各マスの状態ごとに値を保持するが、
ビットボードではそれぞれの石の種類（オセロの場合は白黒）ごとに値を保持する。

例えば、下図の初期局面は、black = 0x0240, white = 0x0420 となる。
２進数で表記すれば black = 0b0000001001000000, white = 0b0000010000100000 だ。


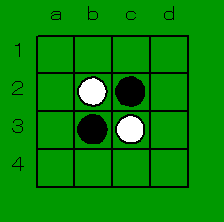
図1. 4×4 オセロ初期局面

4×4 オセロの場合は、マスの数は16なので、unsigned short 型で黒・白の状態を表すことができる。
unsigned short black, white;
typedef unsigned short ushort; と宣言しておけば、型名を簡潔に書ける（以下 ushort を用いる）。
または、github のソースのように typedef unsigned short bitboard_t; と宣言するのもいいかもしれない。

実際のコードでは各座標位置のビット値を宣言しておき、そのシンボルを用いるのがわかりやすくてよい。

#define     A1      0x8000
#define     B1      0x4000
#define     C1      0x2000
.....
#define     D4      0x0001
.....
ushort black = B3|C2, white = B2|C3;    //  初期局面

将棋や囲碁ではマスの数が2のべき乗ですらないので無駄が生じるが、
オセロ、チェス、チェッカーは8×8サイズなので
丁度64ビット変数2つで盤面を表すことができ、無駄がなく効率的だ。
オセロやチェスなどのボードゲームでは、マスの数だけの配列で盤面を表すことが多い。
4×4 オセロであれば、要素数16の配列を用意すればよい。

    char board[4][4];   //  4x4 オセロの盤面

または１次元配列で、添字計算を自前で行っても良い。

    char board[4*4];    //  4x4 オセロの盤面

ビットボードの場合は、4バイトのメモリしか使用しないが、配列であれば16バイト必要だ。4倍の差がある。
ビットボードはメモリ使用量が少ないことが利点のひとつだが、
次章で説明するいくつもの高速なアルゴリズムが使用でき、コードの実行が格段に高速になる。
欠点としては、ビット演算を多用するので、慣れていない人にはコードが理解しづらくなる点だ。
慣れていない人は、本稿を機会に、ぜひビット演算をマスターしてほしい。

ちなみに、筆者がビットボードのことを知ったのは2000年頃だったと思う。その頃発明された
のだろうとずっと思っていたのだが、調べてみると初めて使用されたのは、1950年代に Samuel
により開発されたチェッカープログラムでだった。あまりに古くてびっくりした。
参照： https://en.wikipedia.org/wiki/Bitboard#History

アルゴリズム

以下、4×4オセロ完全解析のためのビットボードを使用する各種アルゴリズムについて解説する。

空白があるかどうかの判定

まずは小手調べとして簡単なアルゴリズム、盤面に空白があるかどうかの判定だ。
オセロでは盤面に空白が無くなると終局なので、この処理が必要になる。
下記は１次元配列データ構造で、ループを使う版：

#define     EMPTY       0
//  空欄がなければ true を、そうでなければ flse を返す
bool isBoardFull(const char *board) {
    for(int i = 0; i < 16; ++i) {
        if( board[i] == EMPTY )     //  空欄を発見した場合
            return false;
    }
    return true;    //  空欄が無かった場合
}

下記はビットボードを使用する版：

//  空欄がなければ true を、そうでなければ flse を返す
bool isBoardFull(ushort black, ushort white) {
    return ~(black|white) == 0;
}

ビットボード使用版はループが無く、しかも2回の論理演算と1回の比較だけで、
実行命令が少なく、配列版に比べると非常に高速だ。
現在のCPUは機械語命令デコードが多段化し、分岐予測・投機実行を行っているので、
分岐予測が外れると、命令デコードをやりなおす必要があり、何クロックも無駄に費やしてしまうことがある。
ビットボードを使うとそもそも条件分岐が無いので、その点でも実行が高速になるという仕組みだ。

石数の数え上げ

次は石数の数え上げた。ここからちょっと難しくなるかもしれないが、がんばってついてきてほしい。
オセロの勝敗は終局時の石数差で決まるので、石数を数え上げる処理は大変重要だ。
ビットボードの場合は、石がある箇所のビットが１、ない箇所が０なので、
１の箇所（ビットの値が１であることを、ビットが立っているとも言う）を数えればよい。

素直にビット数分ループを行い、立っているビットを数えるプログラムは以下のようになる。

//  立っているビット数を数える。ループを用いる版（処理時間は O(N)）
int numOfBits(ushort bb)
{
    int count = 0;
    for(ushort mask = 0x8000; mask != 0; mask >>= 1) {
        if( (bb & mask) != 0 )
            ++count;
    }
    return count;
}

データ全体のビット数だけループするので、処理時間は、データ全体のビット数をNとすると O(N)。
つまり全体のビット数に比例する。

次はビット演算を用いるアルゴリズム。
下図の様に最初に隣り合う2ビットごとにビット数を数え、次は4ビット、
その次は8ビットと増やしいくことで 値が１のビット数をカウントすることができる。
処理時間は O(logN) となる。16ビットの場合は4回処理すればOKだ。

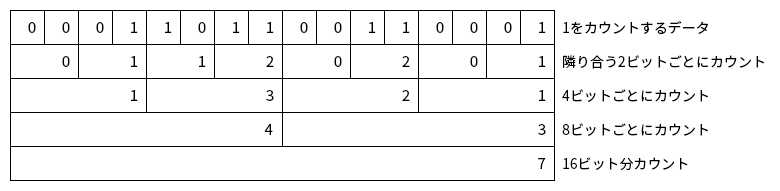
ビット演算により、ループを使わずにビット数を数えるコードを以下に示す。

//  立っているビット数を数える。ビット演算を用いる版（処理時間は O(logN)）
ushort numOfBits(ushort bits)
{
    bits = (bits & 0x5555) + ((bits >> 1) & 0x5555);    //  2bitごとに計算
    bits = (bits & 0x3333) + ((bits >> 2) & 0x3333);    //  4bitごとに計算
    bits = (bits & 0x0f0f) + ((bits >> 4) & 0x0f0f);    //  8bitごとに計算
    return (bits & 0x00ff) + ((bits >> 8) & 0x00ff);    //  16ビット分を計算
}

ビット数が少ない場合は、ループを用いる版と処理速度に大差はないが、ビット数が多くなるほど有利になる。
条件分岐が無いので、投機実行に失敗することもなく、常に一定のクロック数でビット数を数えることができる。

最初の2bitごとの計算部分を場合分けすると、
00 → 00、01 → 01、10 → 01、11 → 10となればいいので
bits = bits – ((bits >>1) & 1); としてもよい。こうすれば論理演算が１回減る。
また、8ビットの場合の最大値は８であり４ビットに収まるので、
最後の16ビット分の計算はマスク処理をひとつ省略できる。

//  立っているビット数を数える。ビット演算を用いる版（処理時間は O(logN)）少し最適化
ushort numOfBits(ushort bits)
{
    bits = bits - ((bits >> 1) & 0x5555);
    bits = (bits & 0x3333) + ((bits >> 2) & 0x3333);
    bits = (bits & 0x0f0f) + ((bits >> 4) & 0x0f0f);
    return (bits + (bits >> 8)) & 0x001f;
}

上記関数を使って白・黒両方の石を数えるには関数を2回呼ぶ必要があるが、
両方の状態を 32ビットにパックすれば、より少ない時間でそれぞれの個数を数え上げることができる。

//  白石・黒石の立っているビット数を同時に数える。
void numOfBits(ushort &b, ushort &w)    //  カウントはそれぞれの変数に代入して返す
{
    uint bits = (b << 16) | w;
    bits = bits - ((bits >> 1) & 0x55555555);
    //bits = (bits & 0x55555555) + ((bits >> 1) & 0x55555555);
    bits = (bits & 0x33333333) + ((bits >> 2) & 0x33333333);
    bits = (bits & 0x0f0f0f0f) + ((bits >> 4) & 0x0f0f0f0f);
    bits = (bits & 0x00ff00ff) + ((bits >> 8) & 0x00ff00ff);
    b = (ushort)(bits >> 16);
    w = (ushort)bits;
}

関連記事

投稿が見つかりません。

筆者：津田伸秀
プロフィール：テニス・オセロ・ボードゲーム・パズル類が趣味の年齢不詳のおじさん。 自宅研究員（主席）。vi と C++が好き。迷走中・・・ ボードゲーム・パズル系アプリ開発・リリースしてます。
4x4 オセロ完全解析【第2回】
一覧へ戻る