今回は【基礎理論(アルゴリズム)編】木構造について紹介します。
木構造を学ぶにあたっては、“木構造の構成要素”と“木構造の種類”の2つを覚える必要があります。
字面だけでは覚えづらいので、適宜イラストを参照しながら理解を深めていってくださいね!
木構造について
木構造とは、親から子にかけて枝分かれした階層構造をもつデータ構造になります。
木構造のような階層構造においては、枝分かれ元が親、枝分かれ先が子と呼ばれます。(家系図みたいですね!)
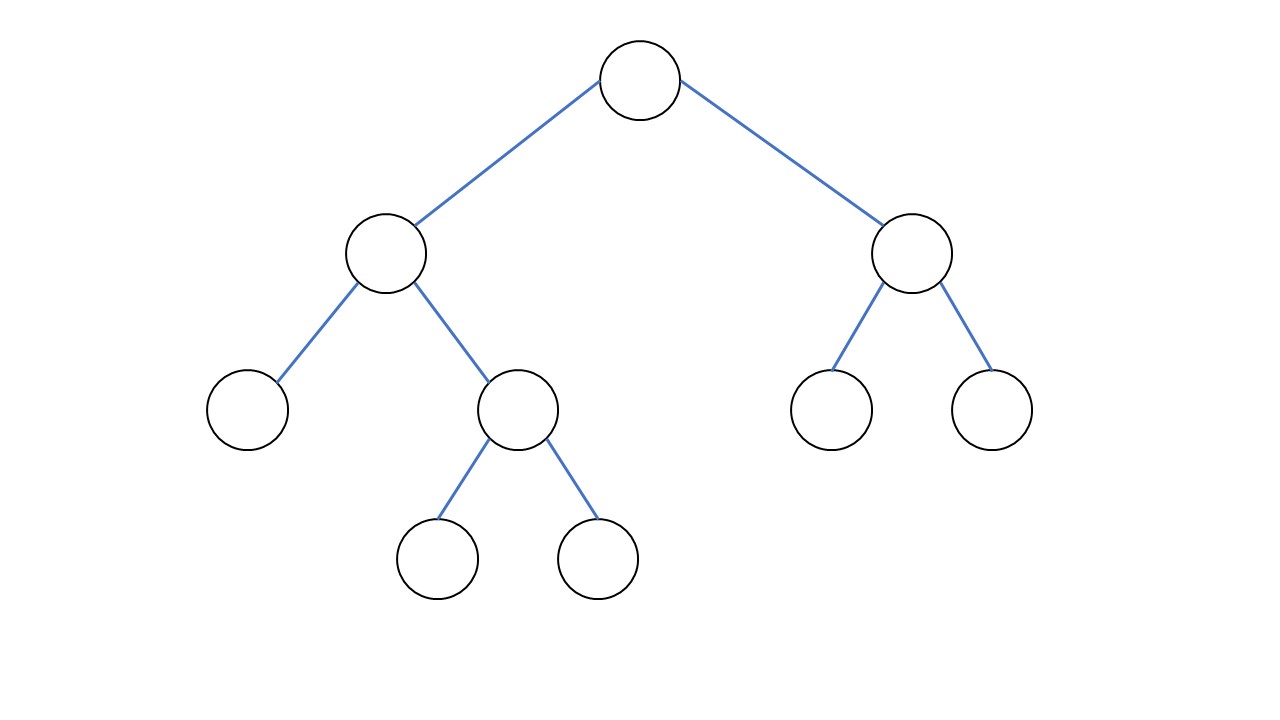
まずはイメージ図を参照してみましょう。
このイメージのように、上から下にかけて木のように枝分かれしていくのが木構造の特徴になります。
ちょうど木をさかさまにしたような状態に似ているので木構造という名称になっているのですが、
それぞれの要素(〇の部分)には次のように名前が割り振られています。
- 各要素:節(ノード)
- 節の中でも親をもたない要素(一番上のデータ):根(ルート)
- 節の中でも子をもたない要素(一番下のデータ):葉(リーフ)
また、それぞれの要素を結ぶ線は枝(ブランチ)と呼ばれます。
木をイメージすれば名前は直ぐに覚えられそうですね!
ここで、もう一つ覚えてほしいワードとして、部分木と深さというものを紹介したいと思います。
まずは部分木について説明します。
木構造は単純な構造なので、ある節から下をまるごと切り取っても、同じように木構造が生まれたりします。
(切り取る節が新しい木構造の根になるイメージです)
こうして元の木構造の“一部”に見つけられる木構造のことを部分木と呼ぶことにしています。
ちなみに、ある節の左側にぶら下がる部分木を左部分木、右側にぶら下がる部分木を右部分木と呼びます。
また、深さとは根から“ある節”までの階層数のことを表しています。
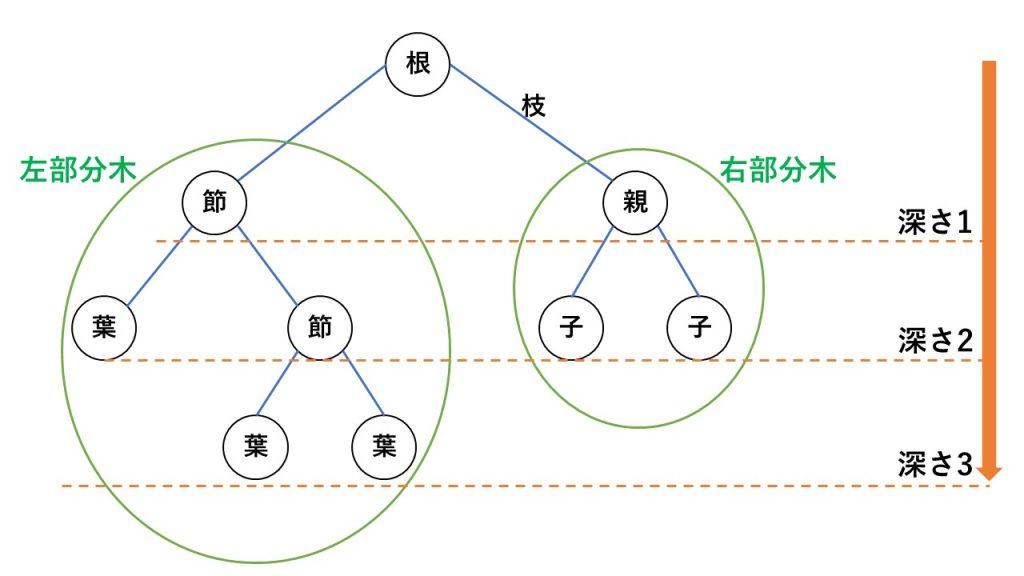
先ほどのイラストを使ってここまでの用語を整理しておきましょう。
イラストの中ではそれぞれに用語を割り振ってありますが、見方や考え方を変えれば呼び方も変わります。
一番上の“根”と書いてある要素を例にとってもみても、根だけではなく節、親といった捉え方もできますよね。
1枚のイラストにまとめる都合上このように用語を割り振ってありますが、それぞれの意味をよく理解して覚えるようにしてくださいね!
木構造の種類について
ここからは二分木と呼ばれる木構造についてご紹介していきたいと思います。
二分木とは、全ての親が1つか2つの子しかもたない木構造のことを指します。
3つ以上に枝分かれすることのない木構造を二分木と呼んでいるんですね!
今回はこの二分木と呼ばれる種類の木構造から、完全二分木、二分探索木を説明します。
まずは完全二分木についてです。
完全二分木は、全ての葉の深さが等しい二分木を表します。
ただし、深さが1だけ異なる葉がある場合にも、要素が左から詰めるように配置されている場合は完全二分木と呼ばれます。
次のイラストを見てみましょう。
左と右、どちらの木構造も完全二分木と呼ばれます。
データを常に左から均等に割り振っていけば完全二分木を作ることができますね。
次は二分探索木についてです。
二分探索木は、全ての要素が「左の子の値<親の値<右の子の値」という制約にしたがって配置された二分木のことを指します。
この木構造は、二分探索(バイナリーサーチ)と呼ばれる比較的高速なデータ検索に用いられる二分木です。
親の値と探したい値を比べて、探したい値の方が小さければ左部分木に、大きければ右部分木に移動することで、
根から葉に向かって進むたびに検索対象数を大幅に減らしていくことができます。
基本情報技術者試験では、このほかにもヒープ木などについての問題が出題されます。
ヒープ木は全ての要素が「親>子または親<子」のどちらかの制約に従って配置された二分木ですが、詳しくはソートの際にご説明いたします。
逆ポーランド記法について
ここからは、二分木を使った数学のお話をしたいと思います。
というのも、実は私たちが普段使っている数式は、二分木で表すことができます。
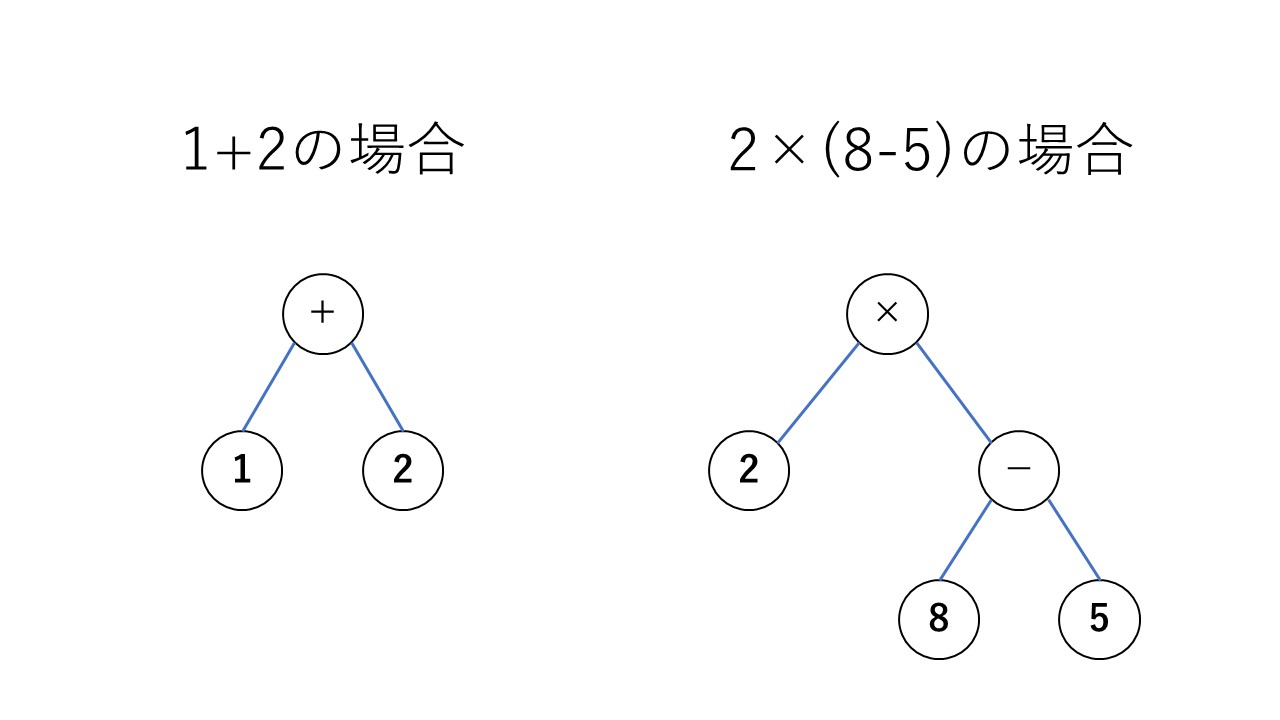
以下の例をご覧ください。
イラストのように、葉に計算したい数字を配置して、それ以外の節に演算子を記述することで、数式を二分木で表現することができます。
逆に言えばこの二分木を読み出していけば数式を取り出すことができるわけですが、その読み出し方にいくつかの種類が存在します。
例えば、左部分木→節→右部分木の順に値を読み出していけば、私たちが普段利用している中置記法と呼ばれる数式を得ることができます。
上のイラストの例でいえば、1+2や2×(8-5)といった式が得られるはずです。
中置記法の例
1+2, (1+3)÷(2+4×3)
それでは左部分木→右部分木→節の順に値を取り出していくと、どういった数式が得られるでしょうか?
上のイラストの例を利用すると、それぞれ12+や285-×といった数式になると思います。
このようにして生まれる、演算子を非演算数(数字)の後に置く数式の記述方法のことを逆ポーランド記法と呼びます。
逆ポーランド記法の例
12+, 13+243×+÷
逆ポーランド記法の場合、左から読んでいけば常に順序通りに計算できる単純な構造になっているので、コンピュータにとって理解しやすいというメリットがあります。(中置記法は()の中身を先に計算する必要がありましたよね…)
逆ポーランド記法の数式を読み解く場合は、左から順に数値を読んでいって、演算子に当たったら直前の2つの数値をその演算子で計算するようにしましょう。
例)
13+243×+÷ (+の直前の1と3で足し算)→4243×+÷(×の直前の4と3でかけ算)
→4 2 12+÷(+の直前の2と12で足し算)→4 14÷(÷の直前の4と14で割り算)→4÷14
さて、最後には木構造を使った数学的なお話までしてみましたが、少しずつ慣れてきましたか?
以上で木構造の紹介は終わりになります。
逆ポーランド記法の計算方法は独特なので、演習を重ねてマスターしておきましょうね!
まとめ
- 木構造は階層構造をもつデータ構造
- 完全二分木、二分探索木、ヒープ木などの種類がある
- 逆ポーランド記法は12+のように演算子を数字の後に置く方法
演習問題
1.木構造に関する記述として最も正しいものを選択してください。
A.子となる要素の“深さ”は親となる要素の“深さ”よりも小さい。
B.要素同士を結ぶ線のことをルートと呼ぶ。
C.ノードには根や葉と呼ばれる種類がある。
D.木構造は常に添え字を用いてデータを管理している。
2.二分木の種類に関する記述として最も正しいものを選択してください。
A.深さが1だけ異なる葉が右詰めで配置されている場合も完全二分木と呼ぶ。
B.ヒープ木は二分探索に使われる木構造である。
C.二分探索木はデータの検索に利用される。
D.二分木とは全ての親が2つの子要素を持つものだけを指している。
3.次の逆ポーランド記法の数式を計算した結果はどれか?
93÷13+2×-
A.-5
B.3
C.6
D.-3
答えは次回の記事で確認してください。
前回の演習問題~解答例
1.解答:D
解説:
A.データへのアクセスに強いのは配列です
B.添え字でアクセスするのは配列です
C.ポインタを辿っていくようにアクセスするので、終端の要素はアクセスに時間がかかります
D.正しい記述です
2.解答:D
解説:
誰からもポインタで参照されない“仙台”というデータが1番目のデータであると考えられます。
ここからポインタを辿っていくと、仙台(次は60)→名古屋(次は100)→沖縄となるので、3番目のデータは“沖縄”になります。
3.解答:X=D, Y=E
解説:
もともとのデータは仙台→名古屋→沖縄→大阪→東京の順になっています。
4番目、すなわち沖縄と大阪の間に博多を挿入したい場合は、博多の後ポインタが大阪を、博多の前ポインタが沖縄を指すようにすればよいことになります。
大阪と沖縄のアドレスはそれぞれ80と100で設定されているので、答えはX=80, Y=100です。